QRコードは人力で読めるのか
夏記事の執筆にあたりQRコードをしくみを実際に読みながら解説してみるのは面白いのでは?と考えた次第ですが、この世の中にはQRコードを人力で読める 変態 ものすごい能力のある人たちがいらっしゃり、これさえ見ればQRコードがなぜ読めるのかは丸わかりとなります。
このほかにも QRコードを人力で読み取る #ネタ - Qiita、QRコードを自力で読み取ってみる|Kaido などなど良記事がたくさんあり、いまさら基本的なQRコードの仕組みを解説してもn番煎じ感が否めないわけであります。
そんな中QRコードでは誤り訂正符号として リード・ソロモン法 なる符号が使われているとのことなので、これなら手垢が付いていないはずだということで解説してみたいと思います。
誤り訂正符号とは
そもそも誤り訂正符号とは、データ伝送に発生する誤りを自動的に検出・訂正するための技術です。送信したいデータに冗長なデータ(パリティ)を加えることで、受信した際にはパリティをヒントに正しいデータを復元することができます。
例えばQRコードが光の反射具合で一部読めなかったり汚れていて白と黒を誤って読んでしまったとしても正しくデータが読めるのはこのためです。
QRコードにおける誤り訂正能力
QRコードの誤り訂正能力は4つのレベルがあり、レベルLで約7%の復元能力、レベルMで約15%、レベルQで約25%、レベルHが最大で約30%となります。
復元レベルに応じてQRコードの見た目も変わり、復元能力が高いほどQRコードの目が細かくなっていきます。
詳しくは QRコードの誤り訂正機能とは?概要から活用方法まで徹底解説 | QR WORLDで解説されています。
リード・ソロモン符号
リード・ソロモン符号はQRコードに限らず、CD/DVD/Blu-rayなどの光学ディスクや地上デジタル放送などに広く用いられる誤り訂正符号です。特に連続して起こるビット誤りに強いのが特徴となります。
本来送りたいデータと、このデータからうまく算出したパリティを付け加えることで受け取ったデータにある程度の誤りがあっても、受け取った側で訂正することができます
ガロア体(有限体)と演算
リード・ソロモン符号では、ガロア体という我々のよく知る世界とはちょっと異なる世界で演算を行います。
- 使用できる文字種: { 0,
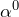 ,
, 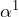 ,
, 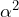 ,
, 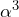 ,
, 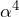 ,
, 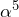 ,
, 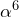 } の計8種類
} の計8種類 - 掛け算のルール:
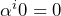 (0は何を掛けても0)
(0は何を掛けても0)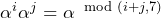 (掛け算は指数の和の7で割った余り)
(掛け算は指数の和の7で割った余り)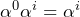 であるので
であるので 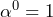 とする(
とする( 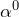 が乗算の単位元)
が乗算の単位元)
- 足し算のルール:
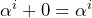 (0で足しても変わらない。0が加算の単位元)
(0で足しても変わらない。0が加算の単位元)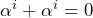 (同じものを足すと0になる)
(同じものを足すと0になる)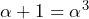 (文字の2次式で表現から和を求められるように設定)
(文字の2次式で表現から和を求められるように設定)
このルールでは、![]() は以下のようにも表現できます。
は以下のようにも表現できます。
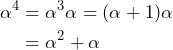
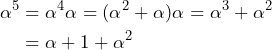
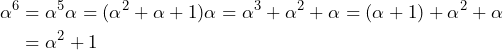
このように各文字は ![]() の2次多項式としても表現でき、その係数をとれば3ビットの数としても表現可能です。
の2次多項式としても表現でき、その係数をとれば3ビットの数としても表現可能です。
まとめると以下の表になります。
| 文字 | 多項式表現 | ビット表現 |
|---|---|---|
| 0 | 0 | 000 |
| 1 | 001 | |
| 010 | ||
| 100 | ||
| 011 | ||
| 110 | ||
| 111 | ||
| 101 |
多項式表現により、任意の文字同士の足し算が行えるようになっています。
例えば ![]() となり、上記の表から
となり、上記の表から ![]() であることがわかります。
であることがわかります。
符号化
(![]() )という文字列を送信してみたいと思います。
)という文字列を送信してみたいと思います。
始めにメッセージ多項式![]() を作ります。これは各桁の文字が係数となる多項式となり、今回なら以下のようになります。
を作ります。これは各桁の文字が係数となる多項式となり、今回なら以下のようになります。
![]()
続いて、生成多項式![]() を定めます。
を定めます。
これは訂正能力が高いほど次数の高い多項式となり訂正能力が1(1文字の誤りを訂正できる)にしたい場合は以下のようになります。
![]()
生成多項式は![]() となるように定めています。
となるように定めています。
最後に符号多項式![]() を求めます。今回では以下のような計算となります。
を求めます。今回では以下のような計算となります。
![Rendered by QuickLaTeX.com \[\begin{aligned}C(x) = M(x)G(x) = &(x^{4} + \alpha^{1}x^{3} + \alpha^{2}x^{2} + \alpha^{3}x^{1} + \alpha^{4})(x^{2} + \alpha^{4}x + \alpha^{3}) \\ = &x^6 + (\alpha+\alpha^4)x^5 + (\alpha^2+\alpha^5+\alpha^3)x^4 \\ &+ (\alpha^3+\alpha^6+\alpha^4)x^3 + (\alpha^4+\alpha^7+\alpha^5)x^2 + (\alpha^8+\alpha^6)x + \alpha^7 \\ = &x^6 + \alpha^2x^5 + \alpha^5x + 1\end{aligned}\]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-537e5a65ff43563be367ffea708b41d9_l3.png)
![]() となったので送信すべき文字列は多項式の係数を取って
となったので送信すべき文字列は多項式の係数を取って
![]()
となります。
復号
受信文字列の多項式を ![]() とすると、 (
とすると、 (![]() ) を誤りなく受信できていれば、
) を誤りなく受信できていれば、![]() となり、
となり、![]() と一致します。
と一致します。
![Rendered by QuickLaTeX.com \[\begin{aligned}C(\alpha) &= M(\alpha)G(\alpha) &= M(\alpha)×0 &= 0 \\ C(\alpha^2) &= M(\alpha^2)G(\alpha^2) &= M(\alpha^2)×0 &= 0\end{aligned}\]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-f1b568781a858f8aa36b6366cbe8b865_l3.png)
となるように生成多項式![]() を定めていることから、
を定めていることから、![]() と
と![]() はどちらも 0 となるハズです。この値をシンドロームと呼びます。
はどちらも 0 となるハズです。この値をシンドロームと呼びます。
実際にシンドロームを計算してみるとすべて 0 となることがわかり、文字列は誤りなく受信できたことになります。
![Rendered by QuickLaTeX.com \[\begin{aligned}S_0 = C(\alpha) &= \alpha^6 + \alpha^2\alpha^5 + \alpha^5\alpha + 1 \\ &= \alpha^6 + \alpha^0 + \alpha^6 + 1 \\ &= 1 + 1 = 0\end{aligned}\]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-25e87f49089b3cf23206498b00507916_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned} S_1=C(\alpha^2) &= (\alpha^6)^{2} + \alpha^2(\alpha^{5})^{2} + \alpha^5(\alpha)^{2} + 1 \\ &= \alpha^5 + \alpha^5 + 1 + 1 = 0\end{aligned}\]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-67f20e72d8ab6a942f95e3281f126e20_l3.png)
復号するためには ![]() を以下のように求めることになります。
を以下のように求めることになります。
x⁴ + αx³ + α²x² + α³x + α⁴ <-- 商 M(x)
_________________________________________________
x²+α⁴x+α³ | x⁶ + α²x⁵ + 0x⁴ + 0x³ + 0x² + α⁵x + 1
(x⁶ + α⁴x⁵ + α³x⁴)
_________________
αx⁵ + α³x⁴ + 0x³
(αx⁵ + α⁵x⁴ + α⁴x³)
_________________
α²x⁴ + α⁴x³ + 0x²
(α²x⁴ + α⁶x³ + α⁵x²)
_________________
α³x³ + α⁵x² + α⁵x
(α³x³ + x² + α⁶x)
_________________
α⁴x² + αx + 1
(α⁴x² + αx + 1)
_________________
0 <-- 余り
![]() であるので、係数を取り (
であるので、係数を取り (![]() ) と復号することができました。
) と復号することができました。
エラーの検出と訂正
一方で (![]() ) と
) と ![]() の箇所を誤って受信した場合はどうなるでしょうか
の箇所を誤って受信した場合はどうなるでしょうか
エラーのある受信多項式は、エラー多項式を![]() とすると、
とすると、![]() と表せます。今回の場合は、
と表せます。今回の場合は、![]() であり、
であり、![]() であることが求められれば、
であることが求められれば、![]() を復元できることになります。
を復元できることになります。
まず![]() のシンドローム計算をすると、
のシンドローム計算をすると、![]() となり、誤りが発生していることがわかります。
となり、誤りが発生していることがわかります。
誤りが発生している次数 i は ![]() として求めることができます。
として求めることができます。
![]() であることから、
であることから、![]() の係数部分に誤りがあることがわかります
の係数部分に誤りがあることがわかります
エラーの値は、![]() として求めることができ、この値を計算すると 1 となります
として求めることができ、この値を計算すると 1 となります
よって、![]() であることがわかったので、
であることがわかったので、![]() を計算すれば誤りの無い文字列
を計算すれば誤りの無い文字列![]() を復元することができました
を復元することができました
むすび
QRコードの誤り訂正技術であるリード・ソロモン符号を具体的に計算してみました。
今回の例で用いたガロア体は ![]() を用いましたが、実際のQRコードでは
を用いましたが、実際のQRコードでは ![]() が採用されているようです。つまり文字としては (
が採用されているようです。つまり文字としては (![]() ) の計256個となり、多項式表現は7次式(8ビット)となるようです。
) の計256個となり、多項式表現は7次式(8ビット)となるようです。
汚れたQRコードを人力で読むのはちょっと無理そうなことがわかりました。
QRコードは(株)デンソーウェーブの登録商標です。
参考
- リードソロモン符号 | 技術説明 | Siglead
- リード・ソロモン符号 - Wikipedia
- 中日新聞:自動車工場のガロア体 QRコードはどう動くか
- 有限体の例: GF(2^4) と GF(2^8) #数学 - Qiita
- 有限体 - Wikipedia

