こんにちは、nozueです。
好きなポケモンはチラチーノです。かわいくて強くてテクニシャンって最高じゃないですか!?
さて、12月は忘年会シーズン。ビンゴ大会が行われることがあるかと思います。
すぐにビンゴになる人がいたり、自分がリーチなのになかなかビンゴにならなかったり、
逆にすぐにビンゴになってラッキー!と思ったりするイベントではないでしょうか。
そんなビンゴゲームをプログラミングしてシミュレーションしてみれば、
どれくらいの抽選回数でビンゴになるのかわかるのではないか!?と思ったので、調べてみました。
※ 途中経過は結構だよ! 結果はよ!はよ!という方はこちら → シミュレーション結果(ページ内リンク)
ビンゴゲームのルール
一般的な5×5のビンゴゲームを想定しています。
以下に箇条書きでルールを書きます。一般的なルールです。
- ビンゴカードには、1~75のうち24個の数字が書いてある。
- ビンゴカードの真ん中のマスは、はじめから消されている。
- 1~75の数字が順番に抽選される。いちど抽選された数字は、ふたたび抽選されることはない。
- 抽選された数字がビンゴカードにあれば、その数字を消す。
- タテ、ヨコ、ナナメのいずれか1列の数字が消されたらビンゴ。
以降、どこか1列が消された状態のことをビンゴと呼び、抽選が行われてビンゴになるまでの一連の流れをビンゴゲームと呼ぶことにします。
このような条件でプログラムを組んでみました↓
プログラム
C言語で組みました。プログラムがキレイでないのはご了承ください(´・ω・`)
100万回ビンゴゲームを行い、[抽選回数(n回), n回でビンゴになったのが何ゲームあるか]の組を出力しています。
このような形式です↓
…
30,19318
31,21389
32,23588
…
// 5x5のビンゴプログラム
// 条件
// ・抽選される数は1~75
// ・カードには1〜25が順番に書かれている。1行目左から1〜5、...、5行目21〜25
// ・真ん中のマスは、はじめから消されている
// ・毎回違う数が抽選される
#include<stdio.h>
#include<time.h>
#define N 1000000
// 抽選する
int draw(int drawn_cnt, int *drawn_num){
int i, continue_fl = 1, shot = 0;
while(continue_fl == 1){
shot = rand() % 75 + 1;
if(drawn_cnt == 0) return shot;
for(i = 0; i < drawn_cnt; i++){
if(drawn_num[i] == shot){
continue_fl = 1;
break;
}
continue_fl = 0;
}
}
return shot;
}
// ビンゴかどうか判断する
int judge(int *shot_fl){
int i, j, shot_cnt_in_line, bingo_cnt=0;
for(i = 0; i < 5; i++){
// タテ
shot_cnt_in_line = 0;
for(j = 0; j < 5; j++){
if(shot_fl[5 * i + j] == 0) break;
shot_cnt_in_line++;
}
if(shot_cnt_in_line == 5) bingo_cnt++;
// ヨコ
shot_cnt_in_line = 0;
for(j = 0; j < 5; j++){
if(shot_fl[i + 5 * j] == 0) break;
shot_cnt_in_line++;
}
if(shot_cnt_in_line == 5) bingo_cnt++;
}
// ナナメ
shot_cnt_in_line = 0;
for(i = 0; i < 5; i++){
if(shot_fl[6 * i] == 0) break;
shot_cnt_in_line++;
}
if(shot_cnt_in_line == 5) bingo_cnt++;
shot_cnt_in_line = 0;
for(i = 0; i < 5; i++){
if(shot_fl[4 * i + 4] == 0) break;
shot_cnt_in_line++;
}
if(shot_cnt_in_line == 5) bingo_cnt++;
return bingo_cnt;
}
int main(){
int i, k;
int card[25], shot_fl[75], drawn_num[75], shot, drawn_cnt, bingo_cnt;
int min=100, max=0, cnt_list[75];
double total_cnt=0, ave;
FILE *fp;
// 初期化
srand((unsigned)time(NULL));
for(i = 0; i < 75; i++) cnt_list[i] = 0;
// N回ビンゴゲームを行う
for(k = 0; k < N; k++){
// 初期化
drawn_cnt=0, bingo_cnt=0;
for(i = 0; i < 25; i++){
card[i] = i + 1;
shot_fl[i] = 0;
}
for(i = 0; i < 75; i++) drawn_num[i] = 0;
// 真ん中を消す
shot_fl[12] = 1;
while(bingo_cnt == 0){
// 抽選
shot = draw(drawn_cnt, drawn_num);
drawn_num[drawn_cnt] = shot;
drawn_cnt++;
// 当たった数字のマスを消す
for(i = 0; i < 25; i++){
if(card[i] == shot){
shot_fl[i] = 1;
break;
}
}
// ビンゴ判定
bingo_cnt = judge(shot_fl);
}
// 集計
total_cnt = total_cnt + drawn_cnt;
if(drawn_cnt < min) min = drawn_cnt;
if(drawn_cnt > max) max = drawn_cnt;
cnt_list[drawn_cnt]++;
}
// 結果をファイルに出力
ave = total_cnt / N;
fp = fopen("result.txt", "w");
fprintf(fp, "ave=%f\n", ave);
for(i = min; i <= max; i++) fprintf(fp, "%d,%d\n", i, cnt_list[i]);
fclose(fp);
}
シミュレーション結果
100万回ビンゴゲームをやった結果です。
あるいは、100万人が同時に1回だけビンゴゲームをやった結果とも言い換えられます。
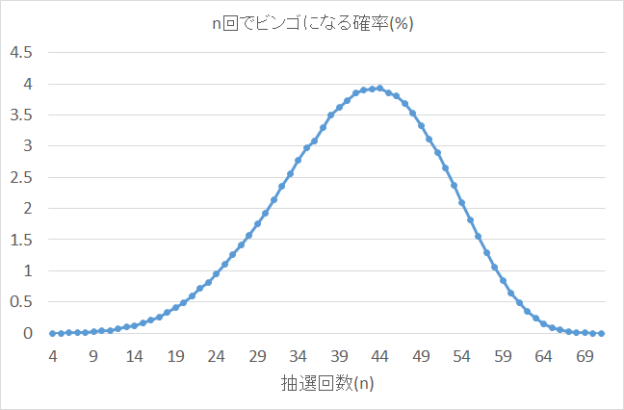
横軸は抽選回数、縦軸はn回でビンゴになる確率(%)です。
平均値は41回、最頻値は45回です。
きれいな正規分布にならずに、右側に寄った形をしていますね。
このグラフからわかるのは、抽選が45回までは徐々にビンゴになる回数が増え、45回でピークを迎えて、その後徐々にビンゴになる回数が減っていくということです。
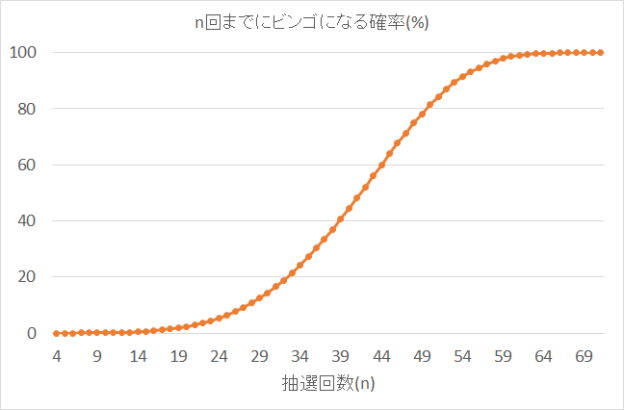
続いて、累積分布グラフです。
この場合の累積分布グラフとは、横軸に抽選回数(n)、縦軸にn回までにビンゴになる確率をとったものです。
nを増やせば増やすほど、縦軸の値が100%に近づいていきます。
適当な値をピックアップしたものが下の表になります。
| 抽選回数 | ビンゴになる確率(%) |
|---|---|
| 34 | 25 |
| 41 | 50 |
| 47 | 70 |
| 50 | 80 |
| 53 | 90 |
| 56 | 95 |
抽選35~50回で傾きが急になっているので、急激に増えていることが分かります。
急にビンゴになる人が増えてきて、ゲームとして盛り上がる仕組みになっているんですね。
おわりに
抽選回数の平均値は意外と多いのだなと感じました。
抽選35回前後でビンゴになるのもたまにはあるよ程度に思っておけば、他の人と比べて焦ったりすることがないのかなと思いました。
おまけ
おまけが本編だと思った?
早くビンゴになったら景品がもらえるよ!という場合に、どれくらいの確率で景品をゲットできるのでしょうか?
参加者は誰もがビンゴになる確率は同じです。(そうでないと不公平なゲームになる)
なので、今回のシミュレーションとは関係なく、
景品数 / 参加者数
で求められます。
参加者10人に対して景品が10個なら、10/10=100%ですし、参加者10人に対して景品が3個なら、3/10=30%となります。
ただし、抽選40回前後でビンゴになる人が続出するので、ビンゴになったら早く申告してさっさと景品をもらった方が良いですね。景品の数は限られている(ことが多い)ので、もたもたしてるともらいそびれますよ!