前回: (1/16)実は語を1個ずつ後ろに追加しているだけ(翻訳)
🔗 ChatGPTのしくみとAI理論の根源に迫る:(2/16)その確率は「どこから」来たのか?(翻訳)
なるほど、ChatGPTはどんなときも常に確率に基づいて次の語(word)を選んでいることはわかりました。しかし、その確率は一体「どこから」やって来るのでしょうか?
最初はうんとシンプルな問題から考えてみましょう。英文を一度に1文字(1 letter)ずつ(1語ではなく)生成する場合を考えましょう。このとき、1文字進むたびに、次の文字の確率をどう設定してやればよいでしょうか?
最小限の方法は、何らかの英文のサンプルを手に入れて、その中でどの文字(訳注: 以後は文脈に応じて文字をアルファベットと書きます)がどのぐらい出現しやすいかを数える形で調べることです。たとえば、Wikipediaの「cats」の記事に出現する文字ごとの出現頻度を文字数としてカウントしてみると、以下のように、"e"は4279文字で最多、次は"a"で3442文字...といった具合の結果を得られます1。
次に、「dog」に対しても同じことをやってみましょう。
catsとdogsの結果に現れるアルファベットごとの数字は似ていますが、同じではありません("o"は"dog"という語自体に出現するので、"dogs"の記事での出現頻度は当然ながら高くなります)。しかし、十分な量の英文のサンプルをかき集めてくれば、少なくとも「"e"が一番多く、次は"a"が多い...」という点については一貫した結果が得られると予想がつきます。
このようにして得られた文字ごとの確率を使って、何の工夫もせずに単純に文字のシーケンスを生成すると、以下のようなわけの分からない文字列が得られます。
ここでひと工夫して、文字の間に何らかの適当な確率でスペース文字を加えると、以下のように文字列を少し「語」らしいものに分割できます(語の長さはめちゃくちゃですが)。
この「語の長さ」の分布を、常識的な英単語の長さに強制的に一致させると、以下のように、もう少しマシな「語」っぽいものを作れます。
上の例では、「たまたま」まともな英単語はどこにも出現していませんが、それでも結果は少しは改善されています。
しかしもっと英文らしくするには、アルファベットを漫然とランダムに選んでいるだけではダメで、もっと工夫する必要があります。たとえば、英語の場合、"q"というアルファベットの次には普通は"u"しか来ないことがあらかじめわかっています。
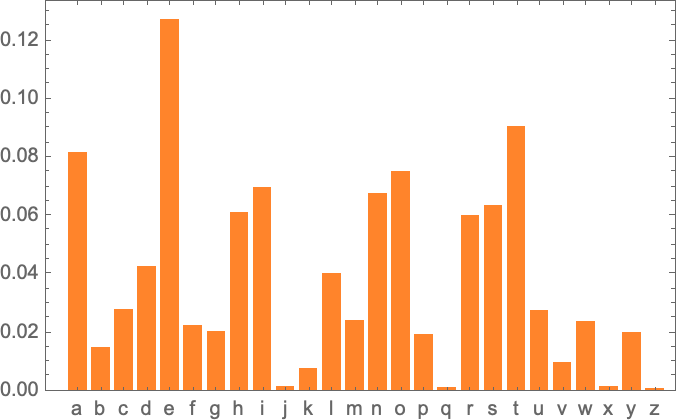
以下は、アルファベットごとの出現確率(出現しやすさ)をプロットしたグラフです。
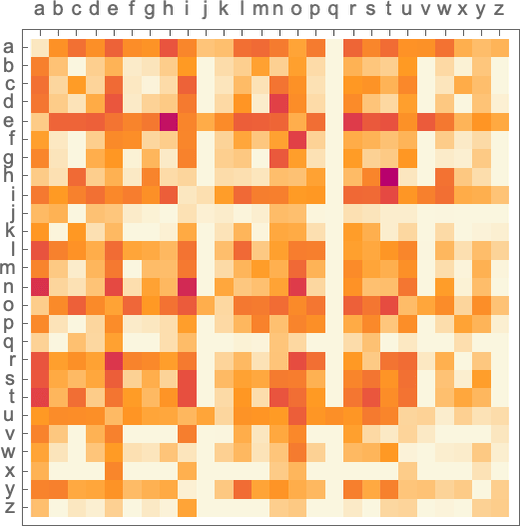
そして以下は、典型的な英文に含まれるアルファベット2文字のペア(これを2-gramと呼びます)の確率をプロットしたグラフです。グラフの横軸は1文字目のアルファベット、グラフの縦軸は2文字目のアルファベットを表しています。そして、1文字目と2文字目のペアが英文に出現しやすいほど、1文字目と2文字目(つまり縦と横)の交点の色が濃くなります。
このグラフを見てみると、たとえば横軸の"q"の列を縦に見ていったときに、縦軸の"u"行に相当する部分以外は、ぜんぶ真っ白になっている(つまり、"q"で始まると、"q"と"u"ペア以外の組み合わせの確率はゼロになる)ことがわかります。
では今度は、先ほどのように語を1文字単位で生成するのではなく、ここに示した「2-gram」の確率表を用いて、語を2文字単位で生成してみましょう。
この結果得られた以下のサンプルには、実際に得た「語」らしきものが、いくつも含まれています。
十分な量の英文データをかき集めれば、アルファベット1文字の確率や2文字(2-gram)の確率だけでなく、もっと長い文字列の確率もかなり精度良く推定できるようになります。そして、「ランダムな語(random word)」を生成するときの確率の元となる単位文字数を、この調子で徐々に増やしていきます(n文字の場合を一般にn-gramと呼びます)。
すると不思議なことに、以下のように単位文字数を0文字から5文字に増やすに連れて、下に行くほど徐々に「本物らしい語」になっていくことがわかります。
しかし今度は、これまでのようにアルファベットの文字単位で確率を扱うのではなく、語全体を元に確率を扱う場合を仮定してみましょう(実際のChatGPTがやっていることもこれと似たようなものですが)。
英語では、一般によく使われる英単語は約4万語あるとされています。ここで、大規模な英文コーパス(数百万冊、数千億語のレベル)を活用すれば、よく使われる英単語が実際の英文でどのぐらいの頻度で使われているかを推定できるのです。
これを利用することで、個別の英単語を、英文コーパスに出現する確率と同じ確率でランダムに選ぶ形で、「文(sentence)」を生成できます。
以下は、実際にそうやって生成した英文のサンプルです。
やはりというか、上の英文の内容はむちゃくちゃで、まるで意味をなしていません。
ではどうすれば改善できるでしょうか?
先ほどはアルファベットの文字単位で確率を考えましたが、そのときと同じ要領で、1個の語の出現確率(出現しやすさ)だけを見るのではなく、さまざまな2つの語の組み合わせ(英単語のペア)や、さまざまな3つの語の組み合わせ、さまざまな4つの語の組み合わせ...という具合に、語数がもっと多いn-gramの組み合わせの確率(出現しやすさ)を考慮すればよいのです。
まずは、さまざまな2つの語の組み合わせ(英単語のペア)の出現確率に基づいて、5つの英文を生成してみたサンプルは、以下のようになります。どの英文も、"cat"で始まっています。
このサンプルをみると、何と、さっきよりも少し「まともな英文」になっています。
ということは、この調子で、十分な個数のn-gramを手に入れて利用すれば「ChatGPTと同じものが手に入る」と予測できそうです。つまり、「まとまった量のまともな文章全体を表す確率」を持つさまざまな語をつなぎ合わせる形で、まとまった量のまともな文章を生成できる「何か」を手に入れられるのではないかと期待する人もいるかもしれません。
しかし問題は、このような膨大な確率を推測するのに十分な量の英文は歴史上一度たりとも存在したことがなく、現代ですら「圧倒的に足りない」ということなのです。
Web世界を隅々までクロールすれば、数千億語レベルの英文を、電子書籍ならさらに数千億語レベルの英文を手に入れられるかもしれません。しかし、よく使われる英単語が仮に4万語あるとすると、4万語の英単語のあらゆる2つを取り出した組み合わせ(ペア)の総数は、それだけで16億(1.6×10^9)2になりますし、さらに、4万語の英単語からあらゆる3つの英単語の組み合わせ(3-gram)を取り出したときの組み合わせの総数は、何と60兆(6×10^13)にも及ぶのです3。
そういうわけで、世の中のありとあらゆるテキストに対して、4万語の英単語からあらゆる2語、3語、4語...n語の組み合わせについて、すべての確率を得ようとするのは、無理な相談なのです。
もっと言えば、たかが20語程度の「文章の切れっ端」程度の英文ですら、それに対して4万語の英単語から取り出したあらゆる2単語の組み合わせ、あらゆる3単語の組み合わせ、あらゆる4単語の組み合わせ...という調子で、あらゆるn単語の組み合わせに関する確率をまともに得ようとすると、その個数は宇宙にあるすべての素粒子の個数をも上回ってしまうため、すべての語に関する、ありとあらゆる組み合わせを網羅したデータを手に入れるのは、絶対に不可能なのです4。
何か方法はないものでしょうか?
ここで重要なのは、すべての組み合わせを大真面目に網羅することではなく、語の組み合わせがどのような確率で出現するかを、「膨大なコーパスの中に実際には存在していなくても」推定可能にするためのモデル(model)を作り上げることです5。
ChatGPTの中核をなすのは、まさにこのような確率を適切に推定するために構築された、いわゆる大規模言語モデル(LLM: Large Language Model)なのです。







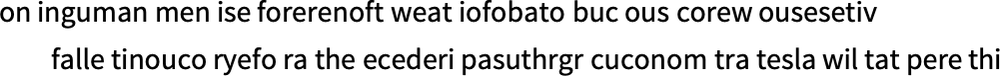



概要
原文サイトのCreative Commons BY-NC-SA 4.0を継承する形で翻訳・公開いたします。
日本語タイトルは内容に即したものにしました。原文が長大なので、章ごとに16分割して公開します。
スタイルについては、かっこ書きを注釈にする、図をblockquoteにするなどフォーマットを適宜改善し、文面に適宜強調も加えています。
元記事は、2023年2月の公開時点における、ChatGPTを題材とした生成AIの基本概念について解説したものです。実際の商用AIでは有害コンテンツのフィルタなどさまざまな制御も加えられているため、そうした商用の生成AIが確率をベースとしつつ、確率以外の制御も加わっていることを知っておいてください。
本記事の原文を開いて、そこに掲載されている図版をクリックすると、自分のコンピュータでもすぐに実行して試せるWolfram言語コードが自動的にクリップボードにコピーされるようになっています。
コモンズ証 - 表示 - 非営利 - 継承 4.0 国際 - Creative Commons