Ruby: 機械学習などで使われる距離測定アルゴリズムをRubyで実装する(翻訳)
機械学習や人工知能の分野は、基本的に2点間の距離(distance)を測定する機能に依存しています。本記事では、よく用いられる測定方法のいくつかを紹介し、それらの解釈について説明するとともにRubyで実装する方法を示します。
🔗 はじめに
機械学習がらみのタスクの多くは、エンティティを「特徴(features)のセット」という観点で記述することから始まります。
たとえばテキストベースの学習タスクであれば、おそらく語(word)ごとの出現頻度が特徴となるでしょうし、画像ベースの学習タスクであれば、ピクセルの強度値(intensity value)を最初の特徴として使うでしょう。こうしたエンティティは、機械学習アルゴリズムに適した数値要素の配列として表現するのが普通です。
エンティティをこの形式で表現すると、どのエンティティ同士が「互いに近いか」を考えるときに役に立つことがよくあります。この「近傍(proximity)」という概念は、クラスタリングアルゴリズムや最近傍(nearest-neighbour)アルゴリズム、、推奨値生成アルゴリズムなどで重要です。しかし、2つのベクトルの距離はどうやって算出すればよいでしょうか?
これには複数の異なる方法があるので、それぞれの測定方法を紹介してからRubyでの実装方法を示します。
それでは見ていきましょう。
🔗 ユークリッド距離
ユークリッド距離(Euclidean distance)は、私たちを取り巻く世界の2次元や3次元の経験から導き出される、直感に沿った距離測定ですが、この測定は任意の次元に一般化可能です。
たとえば、![]() 次元の2つのベクトル
次元の2つのベクトル![]() と
と![]() があるとすると、2つのベクトル間のユークリッド距離
があるとすると、2つのベクトル間のユークリッド距離![]() は以下のように表せます。
は以下のように表せます。
(1) ![Rendered by QuickLaTeX.com \[D_{\rm{euclidean}} \left( \mathbf{a}, \mathbf{b} \right) = \sqrt{ \sum_{i=1}^{N} \left( a_{i} - b_{i} \right)^{2}}\]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-4d55e1ac4726982a25b0acde6ab81e4f_l3.png)
この測定は各次元で距離の2乗和の平方根を取ることで、ピタゴラスの定理を単に![]() 次元に拡張したものになっています。
次元に拡張したものになっています。
2次元のユークリッド距離はピタゴラスの定理に従う。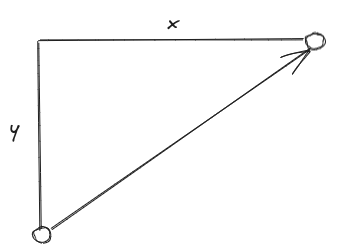
Rubyでの実装はきわめて簡単です。
def self.euclidean_distance(a,b)
return unless a.any? && (a.size == b.size)
diff_squared = (0..a.size-1).reduce(0) do |sum, i|
sum + (a[i] - b[i])**2
end
Math.sqrt(diff_squared)
end
なお、本記事における他の測定も含めた実装(およびspec)については以下のGitHubリポジトリで参照できます。
コードには、両方のベクトルが同じ長さ(=次元)であることを保証するためのガード句がある点にご注意ください。一般に、2つのベクトルが占めている次元空間が異なっている場合は、それらの距離を測定してもあまり意味がありません。同様に、空ベクトルが渡された場合は距離の算出を試みません。
この他の測定についても同様のガード句があります。なお、コサイン類似度やジャッカード距離ではこれと少し異なる条件を課しますが、詳しくは後述します。
🔗 マンハッタン距離
マンハッタン距離(Manhattan distance)は、ある意味ユークリッド距離よりも単純です。2次元において2点をつなぐ経路は、南北に交差する街路(グリッドシステム)のブロックをたどって移動するときの経路と似ているので、「シティブロック距離(City Block distance)」とも呼ばれます。マンハッタン距離では以下のように、移動方向がグリッドシステムの軸方向に制限されます。
マンハッタン距離は「シティブロック距離」とも呼ばれる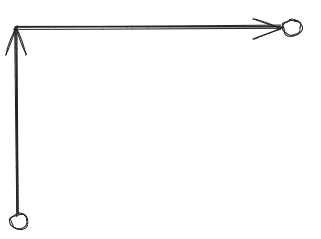
![]() 次元ベクトルにおける
次元ベクトルにおける![]() と
と![]() のマンハッタン距離は
のマンハッタン距離は![]() と記述可能であり、以下のように算出できます。
と記述可能であり、以下のように算出できます。
(2) ![Rendered by QuickLaTeX.com \[D_{\rm{manhattan}} \left( \mathbf{a}, \mathbf{b} \right) = \sum_{i=1}^{N} \left| a_{i} - b_{i} \right| \]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-b48851b498fbe880092e760923fd9f9d_l3.png)
この測定はRubyで以下のように算出できます。
def self.manhattan_distance(a, b)
return unless a.any? && (a.size == b.size)
(0..a.size-1).reduce(0) do |sum, i|
sum + (a[i] - b[i]).abs
end
end
🔗 チェビシェフ距離
チェビシェフ距離(Chebyshev distance)は、1つの次元(点の分離が最大になる次元)のみの分離を考慮します。たとえば、他のすべての座標を1つの軸に集約し、その軸上で点同士の分離の距離を考えるとしましょう。
チェビシェフ距離では、1つの次元の分離のみを考慮する。
点を同一の軸に移動して、その軸上での分離を見つける。
既に確立したベクトル記法を用いると、チェビシェフ距離![]() は以下のように記述できます。
は以下のように記述できます。
(3) ![]()
この測定のRubyにおける実装は以下のようになります。
def self.chebyshev_distance(a, b)
return unless a.any? && (a.size == b.size)
(0..a.size-1).map do |i|
(a[i] - b[i]).abs
end.max
end
🔗 ミンコフスキー距離
ミンコフスキー距離(Minkowski distance)は、これまで既に導入した3つの測定を一般化したものと考えられます。ミンコフスキー測定には![]() という新しいパラメータが導入され、各次元の分離が
という新しいパラメータが導入され、各次元の分離が![]() 乗されます。次に、これらの項をすべての
乗されます。次に、これらの項をすべての![]() 次元で足し上げてから、
次元で足し上げてから、![]() 乗根を取ります。
乗根を取ります。
(4) ![Rendered by QuickLaTeX.com \[D_{\rm{minkowski}} \left( \mathbf{a}, \mathbf{b}, p \right) = \sqrt[p]{ \sum_{i=1}^{N} \left| a_{i} - b_{i} \right|^{p}}\]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-e422e0289d05c27326dd76008508ea83_l3.png)
この測定はRubyで以下のように算出できます。
def self.minkowski_distance(a, b, p)
return unless a.any? && (a.size == b.size)
(0..a.size-1).reduce(0) do |sum, i|
sum + (a[i] - b[i]).abs**p
end**(1.0/p)
end
![]() の場合、ミンコフスキー距離はマンハッタン距離と同一です。
の場合、ミンコフスキー距離はマンハッタン距離と同一です。
![]() の場合、ミンコフスキー距離はユークリッド距離と同一です。
の場合、ミンコフスキー距離はユークリッド距離と同一です。
![]()
![]()
![]()
![]() の極限における
の極限における![]() の同等性についてはそれほど自明ではありませんが、指数
の同等性についてはそれほど自明ではありませんが、指数![]() が大きくなるほど、
が大きくなるほど、![]() は最も差が大きい1個の次元による支配が強まり、他の次元による寄与はますます少なくなることはご理解いただけるかと思います。
は最も差が大きい1個の次元による支配が強まり、他の次元による寄与はますます少なくなることはご理解いただけるかと思います。
私たちのメソッドのspecでは、この制限を以下のように適用できます。
describe "when p = 1_000" do
let(:p) { 1_000 }
let(:examples) do
[
[[0, 1, 2], [1, 2, 0]],
[[0,0], [1,0]],
[[-1,0], [1,0]],
[[0,0,0,0], [1,0,1,0]],
]
end
it "should approach the chebyshev distance" do
examples.each do |vectors|
expect(Metrics.minkowski_distance(vectors[0], vectors[1], p))
.to be_within(0.001).of Metrics.chebyshev_distance(vectors[0], vectors[1])
end
end
end
end
🔗 ハミング距離
ハミング距離(Hamming distance)は、2つのベクトルを要素ごとに比較し、要素が異なる添字ごとに距離を1ずつ増やします。この測定は、文字列や数値を比較するときによく用いられ、2つの配列の添字ごとに要素が同一かどうかだけを比較するので、数値と非数値のどちらの文脈でも適用できます。これは、![]() などの他の測定にはない柔軟性です。
などの他の測定にはない柔軟性です。
たとえば2つの単語間のハミング距離を検討して両者の違いを測定できます(以下の画像ではhappyとhippoを比較しています)。
単語happyと単語hippoのハミング距離は、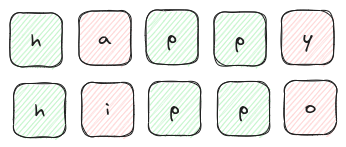
文字の添字が2箇所で異なっているため(赤)、2となる。
この距離測定は、おそらく上の図の方が理解しやすいと思いますが、ある種の数学的厳密性を失わないために![]() を以下のように表記可能です。
を以下のように表記可能です。
(5) ![Rendered by QuickLaTeX.com \[D_{\rm{hamming}} \left( \mathbf{a}, \mathbf{b} \right) = \sum_{i=1}^{N} d_{i} \]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-dd3e67ae830f040fe9512dcfab772b38_l3.png)
ただし
![Rendered by QuickLaTeX.com \[d_i = \begin{cases} 1&(a_i \neq b_i)\\ 0&(\rm{otherwise}) \end{cases}\]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-9a4bcd78274a958efeee815821b9286e_l3.png)
この測定はRubyで以下のように算出できます。
def self.hamming_distance(a, b)
return unless a.any? && (a.size == b.size)
(0..a.size-1).reduce(0) do |sum, i|
sum + ((a[i] != b[i]) ? 1 : 0)
end
end
🔗 コサイン距離
コサイン類似度(Cosine similarity)は、2つのベクトルが指す方向がどのぐらい似ているかを記述します。測定の値は![]() 〜
〜![]() です。
です。
- ベクトルの方向が同じ場合は、
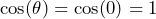
- ベクトルが互いに直行している(=互いに直角)場合は、
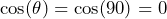
- ベクトルが互いに逆向きの場合は、
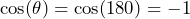
コサイン類似度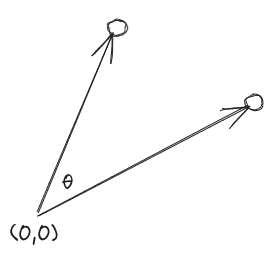
この測定は、関連するベクトルの次元(サイズ)とは無関係であり、ベクトルの向きだけが重要である点にご注意ください。この性質は状況によっては非常に有用であり、ベクトルの正規化が不要になります。
たとえば、テキストの類似度について検討することを考えてみましょう(ここではさまざまなテキストをbag-of-wordsモデルで表現します)。このモデルは、語彙や辞書内にある単語を配列内の個別の添字で表します(この添字はサンプルテキスト内における単語の出現頻度です)。このようにして、個別のサンプルテキストを巨大な(ただし潜在的にはまばらな)頻度の配列で表現します。サンプルテキストは、非常に長い場合もあれば短い場合もありえますが、ここで重要なのは個別の単語の相対的な出現頻度だけなので、コサイン類似度を用いると有意義な比較を行えるようになります。
この測定についても確立済みのベクトル記法で表記可能ですが、ここでは距離ではなく類似性を問題にしているので、類似性の量を![]() で表すことにすると、以下のように表記できます。
で表すことにすると、以下のように表記できます。
(6) ![]()
右辺の分子![]() は、2つのベクトル
は、2つのベクトル![]() と
と![]() のドット積を表し、分母の
のドット積を表し、分母の![]() はベクトル
はベクトル![]() の度合い(長さ)を表します。
の度合い(長さ)を表します。
ここで、ドット積とベクトルの長さ(modulus)をそれぞれ求めるための関数を2つ導入します。
def self.dot_product(a, b)
(0..a.size-1).reduce(0) do |sum, i|
sum + a[i] * b[i]
end
end
private_class_method :dot_product
def self.mod(a)
Math.sqrt((0..a.size-1).reduce(0) do |sum, i|
sum + a[i]**2
end)
end
private_class_method :mod
これで、 ![]() を以下のように算出します。
を以下のように算出します。
def self.cosine_similarity(a, b)
return unless a.any? && (a.size == b.size)
return if is_zero?(a) || is_zero?(b)
dot_product(a,b) / (mod(a) * mod(b))
end
…
def self.is_zero?(a)
a.all? {|i| i == 0 }
end
private_class_method :is_zero?
このとき、ゼロベクトルを識別するユーティリティ関数self.is_zero?も導入している点にご注意ください。このユーティリティ関数は、ベクトルのいずれかがゼロベクトルの場合に問題のある(無意味な)計算を避けるうえで有用です。
![]() は既に述べたように、類似性の測定です。これを距離測定に変換するには、代わりに
は既に述べたように、類似性の測定です。これを距離測定に変換するには、代わりに![]() を検討することが可能です。こうすることで、コサイン距離
を検討することが可能です。こうすることで、コサイン距離![]() は以下のように記述できます。
は以下のように記述できます。
(7) ![]()
つまり、cosine_similarityは既に宣言済みの関数を用いて以下のように実装できます。
def self.cosine_similarity(a, b)
return unless a.any? && (a.size == b.size)
return if is_zero?(a) || is_zero?(b)
1 - self.cosine_similarity(a, b)
end
🔗 ジャッカード距離
ジャッカード指数(Jaccard index)は、(2つの配列ではなく)2つの集合に備わっている特性ですが、同じアイデアを配列のペア全体に渡る一意の項にも適用できます。本記事に登場した中で、長さが等しくないものにも適用可能な測定はこれだけです。
この測定は、2つの集合の交差(つまり集合Aと集合Bの共通集合の要素の個数)と、2つの集合の和集合(つまり集合Aと集合Bの両方で一意に含まれる要素の個数)の比率を調べます。百聞は一見にしかず、以下の図をご覧ください。
ジャッカード指数: 2つの語に共通する異なる文字は2個、両方の語で一意の文字は6個なので、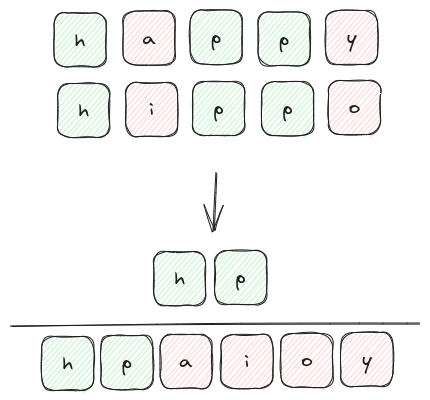
ジャッカード指数は0.33になる。
![]() の場合と同様、ジャッカード指数で考慮されるのは個別の集合のメンバーにおける同一性だけなので、数値でないメンバーにも適用可能です。上の例から、2つの語に含まれる文字の添字を算出する方法がわかります。
の場合と同様、ジャッカード指数で考慮されるのは個別の集合のメンバーにおける同一性だけなので、数値でないメンバーにも適用可能です。上の例から、2つの語に含まれる文字の添字を算出する方法がわかります。
既にお気づきと思いますが、ジャッカード指数は「距離」の測定ではなく「類似性」の測定です。2つの集合が互いに同一の場合は1と評価され、2つの集合に同じ文字が1個もなければ0と評価されます。この指数を距離の測定に変換するには、以下のように![]() を「1 - ジャッカード指数」と定義するだけで住みます。
を「1 - ジャッカード指数」と定義するだけで住みます。
(8) ![]()
この測定はRubyで以下のように算出できます。
def self.jaccard_similarity(a, b)
return unless a.any? && b.any?
1 - (a & b).size / (a | b).size.to_f
end
このRuby配列の集合演算では、&を交差(共通集合)、|を和集合にそれぞれ利用しています。Ruby配列で集合演算を行う方法について詳しく知りたい場合は、以下の過去記事をご覧ください。
参考: Using Set Operations on Ruby Arrays
🔗 まとめ
機械学習アルゴリズムでは、2つのベクトル間の距離を算出する必要が生じることがよくあります(例: 最近傍探索)。本記事では、2つのベクトル間の距離を算出する方法を7種類紹介し、それぞれの測定をRubyでシンプルに実装する方法を示しました。
Rubyでは、そうしたベクトルをArrayクラスでシンプルに表現できます。
意味のある形で測定を適用するために、2つの配列の長さは必ず同じでなければなりません(ジャッカード距離を除く)。
測定に意味があるのは、配列が数値の場合だけであるのが普通ですが、ハミング距離とジャッカード距離はこの限りではありません。
それ以外の測定はすべて2次元や3次元でおなじみの距離(や方向)の概念を拡張したものであり、2つの数値配列の長さ(要素の個数)が等しくなければなりません。
本記事がお役に立てば幸いです。ご意見、質問、訂正などありましたら、お気軽に原文までコメントをどうぞ。
最新の記事をすぐお読みになりたい方は、フォームにて購読をお申し付けください。
🔗 参考
- データサイエンスにおける9つの距離測定
- データサイエンスが知っておくべき7つの距離測定
- A Gentle Introduction to the Bag-of-Words Model - MachineLearningMastery.com(テキストデータのbag-of-wordsモデルを解説するブログ記事)
- distance-measures-in-ruby(本記事で扱った測定を実装したシンプルなGitHubリポジトリ)

概要
元サイトの許諾を得て翻訳・公開いたします。
日本語タイトルは内容に即したものにしました。
metricsの訳語は原則として「測定」としています。