Tech Racho エンジニアの「？」を「！」に。
  1. TOP
  2. Ruby / Rails以外の開発一般
  3. CPUキャッシュがGoのコードに与える影響（翻訳）
  • Ruby / Rails以外の開発一般

CPUキャッシュがGoのコードに与える影響（翻訳）

概要

原著者の許諾を得て翻訳・公開いたします。

日本語タイトルは内容に即したものにしました。

Goに限らず、CPUのL1/L2/L3キャッシュの挙動を理解するうえでとてもよい記事だと思います。

CPUキャッシュがGoのコードに与える影響（翻訳）

追記（2020/06/29）ご指摘をいただき以下の訳文を修正いたしました。ありがとうございます！

Jackie Stewartによると、これまで3度チャンピオンに輝いた某F1レーサーはこれまで3度チャンピオンに輝いたF1レーサーJackie Stewartは、自動車の内部動作を十分理解することで運転技術が向上したそうです。

レーサーになるためにエンジニアになれとは言わない。レーサーに必要なのは「マシンの気持ちを理解し、マシンの気持ちに寄り添う」ことだ。

LMAX Disruptorを設計したMartin Thompsonは、この「マシンの気持ちに寄り添う」というコンセプトをプログラミングに応用しました。要するに、開発者がソフトウェアを背後で支えているハードウェアを理解することで、アルゴリズムやデータ構造などを設計するときのレベルがアップするはずだという考え方です。

本記事では、プロセッサ（CPU）の内部構造に踏み入り、プロセッサ内部のいくつかの概念を理解しておくと最適化でどのように役立つかについて解説します。

基本について

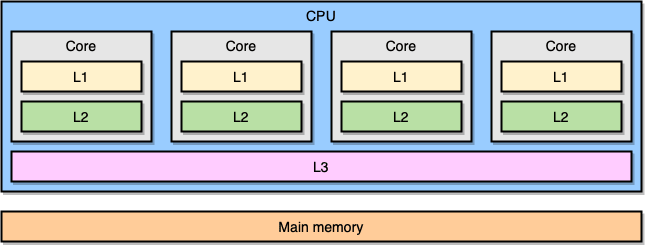
モダンなプロセッサは「対称型マルチプロセッシング（SMP: symmetric multiprocessing）」という概念に基づいて設計されています。この設計では、複数のCPUコアが共有メモリ（メインメモリやRAMとも呼ばれます）に接続されています。また、メモリアクセス速度向上のため、「L1」「L2」「L3」という3つのレベルのキャッシュをプロセッサに内蔵しています。正確なアーキテクチャは、CPUメーカーやプロセッサモデルなどによって異なりますが、最もよく用いられるのは以下のように「L1キャッシュとL2キャッシュをCPUコア内部に配置し、L3キャッシュを全コアで共有する」というモデルです。

SMPアーキテクチャ
キャッシュは以下のように、CPUコアに近ければ近いほどサイズが小さく、かつレイテンシ（待ち時間）も短くなります。

キャッシュ レイテンシ CPUサイクル サイズ
L1アクセス 〜1.2 ns 〜4 32 KB〜512 KB
L2アクセス 〜3 ns 〜10 128 KB〜24 MB
L3アクセス 〜12 ns 〜40 2 MB〜32 MB

繰り返しますが、正確な図はプロセッサモデルによって異なります。ここでは見積もりのため、以下の目安で考えます。メインメモリのアクセスに60ns（ナノ秒）かかり、L1キャッシュへのアクセス速度はその約50倍高速だとします。

さて、プロセッサの世界には「参照の局所性（locality of reference）」と呼ばれる重要な概念があります。プロセッサがメモリ上の特定の場所にアクセスするとき、以下のように予測を立てます。

  • 近い将来、メモリ上の同じ場所にアクセスする可能性が非常に高い
    • これは「時間的局所性（temporal locality）の法則」です
  • 近い将来、メモリ上のその場所からごく近い場所にアクセスする可能性が非常に高い
    • これは「空間的局所性（spatial locality）の法則」です

CPUにキャッシュが存在する理由のひとつが、この時間的局所性です。では空間的局所性を高めるにはどうすればよいでしょうか？答えは、メモリ上の1つの場所を単品でCPUキャッシュにコピーするのではなく、「cache line」という単位でCPUキャッシュにコピーすることです（cache lineとは、メモリ上での連続セグメントのことです）。

cache lineのサイズは、キャッシュのレベルによって（もちろんプロセッサモデルによっても）異なります。たとえば以下を実行すると自分のコンピュータのL1キャッシュサイズを表示できます。

$ sysctl -a | grep cacheline
hw.cachelinesize: 64

プロセッサは、変数ひとつをL1キャッシュにコピーするのではなく、64バイトの連続セグメントをL1キャッシュにコピーします。たとえば、Go言語のスライスのint64要素を1個だけコピーするのではなく、その要素以外に7つのint64要素もまとめてコピーします。

Go言語におけるcache lineの具体例

CPUキャッシュのメリットがよくわかる具体例を見てみましょう。以下のコードでは、要素がint64の正方行列2つを結合します。

func BenchmarkMatrixCombination(b *testing.B) {
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i++ {
            for j := 0; j < matrixLength; j++ {
                matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
            }
        }
    }
}

matrixLengthに64kを設定すると以下の結果が得られます。

BenchmarkMatrixSimpleCombination-64000                     8  130724158 ns/op

今度は、matrixB[i][j]を追加するのではなくmatrixB[j][i]を追加してみましょう。

func BenchmarkMatrixReversedCombination(b *testing.B) {
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i++ {
            for j := 0; j < matrixLength; j++ {
                matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
            }
        }
    }
}

さて、結果は変わるでしょうか？

BenchmarkMatrixCombination-64000                           8  130724158 ns/op
BenchmarkMatrixReversedCombination-64000                   2  573121540 ns/op

かなり大きな違いです！これをどう説明すればよいでしょうか？

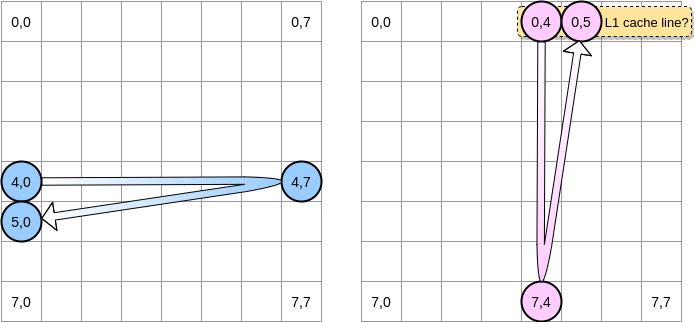
ここで何が起こっているかを図示してみましょう。青い丸は、1番目の行列にあるポインタ、ピンクの丸は2番目の行列にあるポインタです。matrixA[i][j] = matrixA[i][j] + matrixB[j][i]を実行するとき、青ポインタが(4,0)を指していると、ピンクポインタは(0,4)を指します。

この図で使う行列は横座標と縦座標を持ち、左上隅が(0,0)を表します。行列の各行はメモリ上で連続的に配置されます。ここでは明確さを保つため、あえて数学的表現を用いることにします。
さらに、以後の例で使っている行列のサイズは、cache lineサイズの倍数とします。つまり、cache lineが隣の行を「追い越す」ことはありません。

2つの行列はどのように列挙されるでしょうか。青ポインタは右に1つずつ進み、右端の列に到達すると次の行の(5,0)に進む、という具合になります。逆に、ピンクポインタは下に1つずつ進み、下の行に到達すると次の列に進みます。

ピンクポインタが(0,4)にアクセスすると、プロセッサはその行をまるごとキャッシュに乗せます（この例ではcache lineのサイズが4要素分になります）。このとき、ピンクポインタが(0,5)に到達したら、この変数は既にL1キャッシュに乗っているとみなせるでしょうか？

答えは「行列のサイズに依存する」です。

  • 行列のサイズがL1キャッシュのサイズに比べて十分小さい場合は、イエス
    • つまり(0,5)は既にキャッシュに乗っている
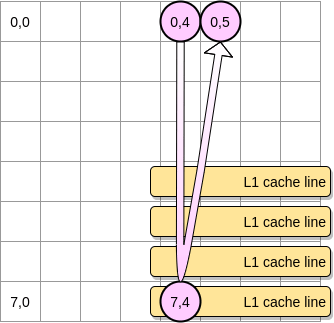
  • そうでない場合、ポインタが(0,5)に進む前に、cache lineがL1キャッシュから追い出される
    • すなわち「キャッシュミス」が発生し、プロセッサは別の方法（L2キャッシュなど）で変数にアクセスしなければならなくなる

キャッシュミスが発生するときのステートは以下のようになります。

L1キャッシュが効くためには、行列のサイズをどのぐらい小さくすべきでしょうか？ここで算数のお時間です。まずL1キャッシュのサイズを知る必要があります。

$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768

著者のPCでは、L1キャッシュが32768バイト、L1のcache lineは64バイトです。つまり、L1に乗せられるcache lineの数は最大で32768/64=512個となります。では、要素が512個の行列で同じベンチマークを走らせてみたらどうなるでしょうか？

BenchmarkMatrixCombination-512                1404     718594 ns/op
BenchmarkMatrixReversedCombination-512        1363     850141 ns/opp

先ほどの結果（64kの行列では300%以上低速）に比べればギャップは縮まりましたが、まだ小さな違いが残っています。何かおかしな点があるのでしょうか？このベンチマークでは行列を2個使っているので、CPUはどちらの行列についてもcache lineを保存しなければなりません。理想的な環境（他のアプリケーションが動いていないなど）であれば、L1キャッシュの50%は1番目の行列で埋まり、残りの50%は2番目の行列で埋まります。今度は、行列のサイズを2で割って要素数256個でやってみるとどうなるでしょうか？

BenchmarkMatrixCombination-256                5712     176415 ns/op
BenchmarkMatrixReversedCombination-256        6470     164720 ns/op

今度はやっと、2つの結果が（ほぼ）同じになりました。

2番目のベンチマークの結果が1番目よりもわずかに速い理由は何でしょうか？この違いは極めて微妙で、Goが生成するアセンブリコードに関連しているように見えます。2番目の場合、2つ目の行列にあるポインタはLEA（Load Effective Address）という別のインストラクションで管理されています。プロセッサがメモリ上のある場所にアクセスする必要が生じると、仮想メモリから実メモリへの変換が発生します。たとえば、int64スライスの要素を管理していて、その最初の要素へのアドレスを既に持っているとします。このときの2番目の要素のアドレスは、LEAを用いてポインタを8バイトずらすだけで読み込めます。本記事のコード例で2番目のテストが速い潜在的な理由がこれである可能性もあります。著者はアセンブリコードの専門家ではないので、皆さまはご自由に分析なさってください。ご覧になりたい方は、1番目の関数と2番目の関数（逆の処理）のアセンブリコードをアップロードしてありますので、そちらをどうぞ。

さて、巨大な行列の場合、プロセッサのキャッシュミスの影響を抑えるにはどうすればよいでしょうか？そのような場合には「loop nest最適化」という手法があり、cache lineのメリットを活かすために、できるだけ与えられたブロックの中だけで列挙する必要があります。

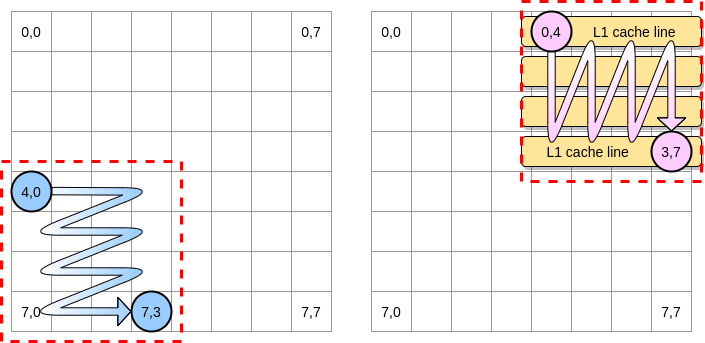
コード例で、要素4つの2乗としてブロックをひとつ定義してみましょう。1番目の行列では、(4,0)から(4,3)までを列挙してから、次の行に処理を進めます。したがって、2番目の行列では(0,4)から(3,4)までを列挙してから次の列に進むことになります。

ピンクポインタが1行目を列挙すると、プロセッサはそれに対応するcache lineを保存します。つまり、ブロックの残りの部分を列挙するときにL1キャッシュが効くということです。

このアルゴリズムをGoで実装してみましょう。しかしその前に、ブロックのサイズを注意深く決めておく必要があります。先の例では、ブロックのサイズはcache lineと等しくなっており、これより小さくなってはいけません。さもないと、アクセスできない要素をcache lineに保存してしまいます。Goのベンチマークでは、int64という要素（8バイト）を保存します。このcache lineは64バイトなので要素を8つ保存できます。つまり、ブロックサイズの値は8以上にすべきということになります。

これで、行列の行と列を端から全部列挙したときと比べて、実装が67%も高速になりました。

BenchmarkMatrixReversedCombination-64000          2  573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000  6  185375690 ns/op

以上が、CPUキャッシュの動作を理解し、より効率的なアルゴリズムの設計に役立つ最初のコード例です。

「false sharing」問題

これで、プロセッサが内部キャッシュを管理する方法についての理解が進んだはずです。軽くおさらいしておきましょう。

  • プロセッサは空間的局所性の法則に従って（単純な1個のメモリアドレスではなく）cache lineを保存する。
  • L1キャッシュは、そのCPUコアと同じ場所に存在する（CPUコアローカル）。

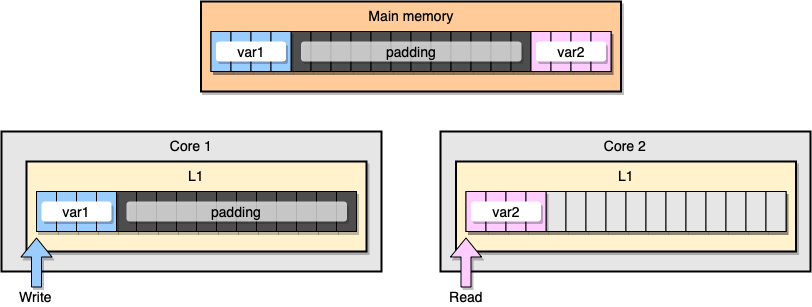
今度は、L1キャッシュの「キャッシュコヒーレンシ（cache coherency）」についてコード例で考えてみましょう。var1とvar2という2つの変数がメインメモリに保存されていて、あるCPUコアの1つのスレッドがvar1にアクセスし、別のCPUコアの別のスレッドがvar2にアクセスするとします。仮に2つの変数がメモリ上で連続（またはほぼ連続）しているとすると、どちらのキャッシュにもvar2が乗るようになります。

L1キャッシュの例
このとき、1番目のスレッドが手元のcache lineを更新するとどうなるでしょう？var2を含むcache lineは、潜在的にはどの部分についても更新される可能性があります。続いて2番目のスレッドがvar2を読み取ると、その値は古いので一貫しなくなってしまう可能性があります。

プロセッサはどのようにしてキャッシュコヒーレンシを維持しているのでしょうか？2つのcache lineが一部の共通アドレスを共有していると、プロセッサはその部分に「shared」とマーキングします。スレッドの1つが「shared」のcache lineを変更すると、2つのcache lineはどちらも「modified」とマーキングされます。キャッシュコヒーレンシを保証するにはCPUコア同士での調整作業が必要になりますが、これはアプリケーションのパフォーマンスを著しく損なう可能性があります。この問題が、いわゆる「false sharing」です。

Goの具体的なアプリケーションを見てみましょう。この例では2つの構造体をたて続けにインスタンス化するので、構造体の配置（アロケーション）はメモリ上で連続するはずです。続いてgoroutineを2つ作成し、それぞれのgoroutineが自分の持つ構造体にアクセスします（Mは100万を表す定数です）。

type SimpleStruct struct {
    n int
}

func BenchmarkStructureFalseSharing(b *testing.B) {
    structA := SimpleStruct{}
    structB := SimpleStruct{}
    wg := sync.WaitGroup{}

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        wg.Add(2)
        go func() {
            for j := 0; j < M; j++ {
                structA.n += j
            }
            wg.Done()
        }()
        go func() {
            for j := 0; j < M; j++ {
                structB.n += j
            }
            wg.Done()
        }()
        wg.Wait()
    }
}

この例では、2番目の構造体の変数nにアクセスするのは2番目のgoroutineだけですが、2つの構造体の配置はメモリ上で連続しているので、変数nはどちらのcache lineにも乗ります（なお、2つのgoroutineがそれぞれ別々のCPUコア上のスレッドで動くと仮定していますが、この場合必須ではありません）。ベンチマークの結果は次のとおりです。

BenchmarkStructureFalseSharing         514    2641990 ns/op

false sharingを防ぐにはどうすればよいでしょうか？ひとつの方法は「メモリパディング（memory padding）」です。メモリパディングの目的は、2つの変数の配置を十分離し、それぞれが別のcache lineに乗るようにすることです。

まず、上述の構造体を作り変えて、変数の宣言後にメモリのパディングを行うようにします。

type PaddedStruct struct {
    n int
    _ CacheLinePad
}

type CacheLinePad struct {
    _ [CacheLinePadSize]byte
}

const CacheLinePadSize = 64

次に2つの構造体のインスタンスを作成し、それら2つの変数に別々のgoroutineでアクセスするようにします。

func BenchmarkStructurePadding(b *testing.B) {
    structA := PaddedStruct{}
    structB := SimpleStruct{}
    wg := sync.WaitGroup{}

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        wg.Add(2)
        go func() {
            for j := 0; j < M; j++ {
                structA.n += j
            }
            wg.Done()
        }()
        go func() {
            for j := 0; j < M; j++ {
                structB.n += j
            }
            wg.Done()
        }()
        wg.Wait()
    }
}

この例は、メモリの観点からは以下のように2つの変数がそれぞれ別のcache lineに乗るようになるはずです。

メモリパディング
結果を見てみましょう。

BenchmarkStructureFalseSharing         514    2641990 ns/op
BenchmarkStructurePadding              735    1622886 ns/op

メモリパディングを行なった2番目のコード例は、最初の実装と比べて40%も高速になりました🎉。ただしこれにはトレードオフが存在します。メモリパディングで実行速度を向上させるには、メモリをもっと割り当てる必要があります。

「マシンの気持ちに寄り添う」は、アプリケーションを最適化するうえで重要なコンセプトです。本記事では、CPUプロセッサの挙動を理解することが実行時間を短縮するうえでどれほど役に立つかについて、さまざまなコード例をご紹介しました。

本記事の構想についてTwitterで素敵な意見を下さったInanc GumusとVal Deleplaceに感謝いたします。お二方のブログも素晴らしい内容ですので、ぜひチェックしてください。

リファレンス

おたより発掘

関連記事

V言語: Goのようにシンプルで、Rustのように小さいバイナリ


タグ
この記事を書いた人

hachi8833

Twitter: @hachi8833、GitHub: @hachi8833 コボラー、ITコンサル、ローカライズ業界、Rails開発を経てTechRachoの編集・記事作成を担当。 これまでにRuby on Rails チュートリアル第2版のコンテンツ監修、Railsガイドのコンテンツ作成を担当。 かと思うと、正規表現の粋を尽くした日本語エラーチェックサービス enno.jpを運営。 実は最近Go言語が好きで、Goで書かれたRubyライクなGoby言語のメンテナーでもある。 仕事に関係ないすっとこブログ「あけてくれ」は2000年頃から多少の中断をはさんで継続、現在はnote.comに移転。Amazonウィッシュリスト: https://bit.ly/32aAmiI

hachi8833の書いた記事一覧へ

本記事の内容へのお問い合せはTwitterで@techrachoへMentionまたはDMにてご連絡頂くか、運営会社であるBPS株式会社のお問い合せフォームよりお問い合せ下さい。

CONTACT

TechRachoでは、パートナーシップをご検討いただける方からの
ご連絡をお待ちしております。ぜひお気軽にご意見・ご相談ください。
CONTACT FORM