Rubyの整数オーバーフローチェックを「スタンプ」で一掃する（翻訳）

Rubyの整数オーバーフローチェックを「スタンプ」で一掃する（翻訳）

Rubyで整数演算のオーバーフロー（桁あふれ）チェックをオフにすることは可能かという質問をRedditで見かけました。質問者は、自分たちの演算がオーバーフローしないことを保証できるので、無意味なチェックでコストを増やさないようにしたいのだそうです。

そのスレッドで他の方が回答していたように、Rubyの標準実装であるMRIでは無理ですが、TruffleRubyなら可能で、かつ安全です。さらに素晴らしいのは、演算がオーバーフローしないことをコードで証明できれば、演算で自動的にそのようになる点です。そしてさらに、コードによる証明がない場合は、標準のRubyを用いて証明を簡単に追加することも可能です。この点にもう少し踏み込めるかどうかを確かめるために、安全性はやや落ちるものの少し高速になるような新しいゼロコストの証明方法を追加してみました。

この方法が実際にパフォーマンス測定可能な形で影響を与えられることを示せます。特に、これが純粋なRubyコードで可能である点は価値があると思います。

このことを述べておく価値がある理由は、最近のコンパイラが一般には気づかれない微妙な形で最適化を行っている見事な例だからです。

オーバーフローのチェック

プロセッサ（CPU）内部では整数演算をハードウェアでサポートしていますが、そこで使える整数は32ビットまたは64ビットなどの固定長です。算術演算の結果がそれより大きくなると、期待と異なる値に丸められてしまいます。Rubyの整数は固定長ではなく、任意の大きさの整数を許容します。では、どうすれば固定長のハードウェアで任意サイズのRuby演算を実装できるでしょうか。これが可能なのは、ハードウェア算術演算の結果があふれるかどうかを検出するしくみがあるからです。これが、今回お話しする「オーバーフローチェック」です。Rubyは、オーバーフローする可能性のあるすべての算術演算の後で、オーバーフローしたかどうかをチェックします。オーバーフローした場合は、任意サイズの整数をサポートするソフトウェアライブラリに切り替えて算術演算をやり直します。

Rubyのサンプルコードをいくつか以下に示します。まずは加算です。

def add_any(a, b, c)
  a + b + c
end

TruffleRubyとGraalでは、コンパイル中のプログラムをグラフデータ構造で表現します。これについては別のところで既に述べましたが、基本的にはコードのフローチャートと思っていただければ結構です。矢印は、制御とプログラム内のデータフローを表します。ボックスは演算や計算を表します。ここでは、Shopifyが開発したSeafoamというツールを用いてグラフをビジュアル表示しています。

以下はRubyのサンプルコードです。T(7)ノード、T(8)ノード、T(9)ノードはそれぞれ a、b、cに対応します。これらの値がIntegerAddExact演算ノード内を流れる様子がグラフからわかります。Exactは、そこでオーバーフローをチェックするという意味です。

生成されたマシン語コードを以下に示します。addとjoというマシン語命令（instruction）があるのがわかります。joは「jump-on-overflow」のことで、得られた結果がハードウェア上の整数として大きすぎる場合にソフトウェアで演算を処理するという意味です。

    0x11bb1f909:    add esi, eax
    0x11bb1f90b:    jo  0x11bb1f9fc
...
    0x11bb1f91f:    add r10d, esi
    0x11bb1f922:    jo  0x11bb1f9de

算術演算のたびに余分なチェックが走っています。これがどれほどよろしくないかは想像がつくでしょう。だからこそこれを排除したいと思うわけです。ここで皆さんに良いニュースと悪いニュースがあります。良いニュースは、ほとんどの人がjo命令の実行コストは非常に低いと指摘していることです。プロセッサはjo命令をうまくパイプライン化するので、この命令自体がパフォーマンスに大きく影響することはありません。悪いニュースの方は、この命令があると演算を効率よくpackできなくなり、それ以上最適化できなくなることです。

スタンプ: コンパイラ内部のマイクロ型

次に進む前に、ここで新しいコンセプトをひとつ紹介しておく必要があります。

Rubyは（最近の静的型関連のアイデアを別にすれば）動的型付け言語ですが、優秀なコンパイラは動的型付け言語をコンパイルするときに自動的に静的型を発見することをご存知でしょうか？上のコードのa、b、cが整数であると認識するような単純なものもありますが、世にほとんど知られていないもうひとつの型、それが「スタンプ（stamp）」です。

スタンプは、コンパイラの内部にだけ存在する一種のマイクロ型です。スタンプは他の型と同様、値に関する情報を表しますが、これまで扱ったような型と異なり、「オブジェクトがnullかどうか」「値が正か負か」「整数のどのビットがオンになっているか」といったさまざまなプロパティを私たちにもたらしてくれます。このプロパティに注目していくことにします。

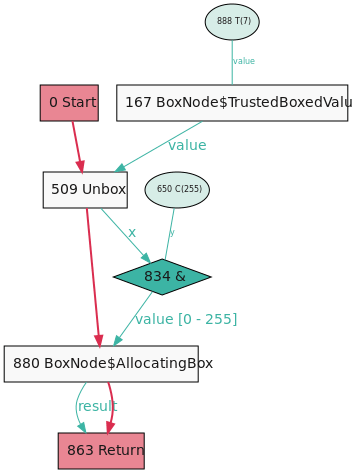
Rubyコードでは、以下のようにビットAND演算子&を用いることでスタンプの例を観察できます。

def stamp(a)
  a & 0xff
end

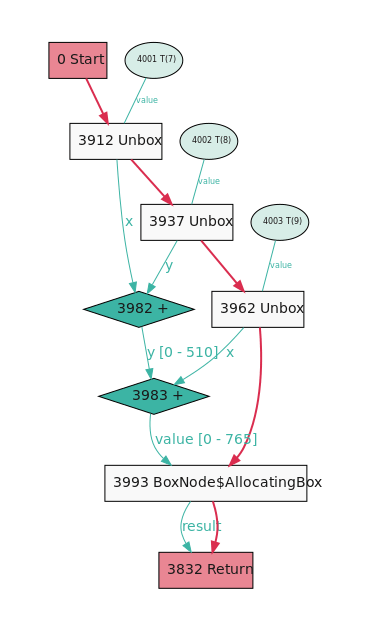
このコードのコンパイラグラフを見ると、ノード834から880に流れる値を表すエッジでスタンプがアノテーションされていることがわかります。このvalue [0 - 255]は、「その値が指定の範囲内に確実に収まる」ことを保証するスタンプがこのエッジにあるという意味です。

スタンプは何のためにあるのでしょうか。ある演算をコンパイルするときに、その演算に流れ込む値のスタンプをチェックし、スタンプが値について保証する内容に基づいてコンパイル方法を変更できます。

ここに「ビッグアイデア」があります。「値は十分小さいのでオーバーフローしない」とスタンプが主張する2つの値を足すと、コンパイラは自動的にオーバーフローチェックを除去できます。そのためには、これらのスタンプを生成するための何らかの証明（proof）が必要です。これについては次に説明します。

ビットマスクによってスタンプを追加する

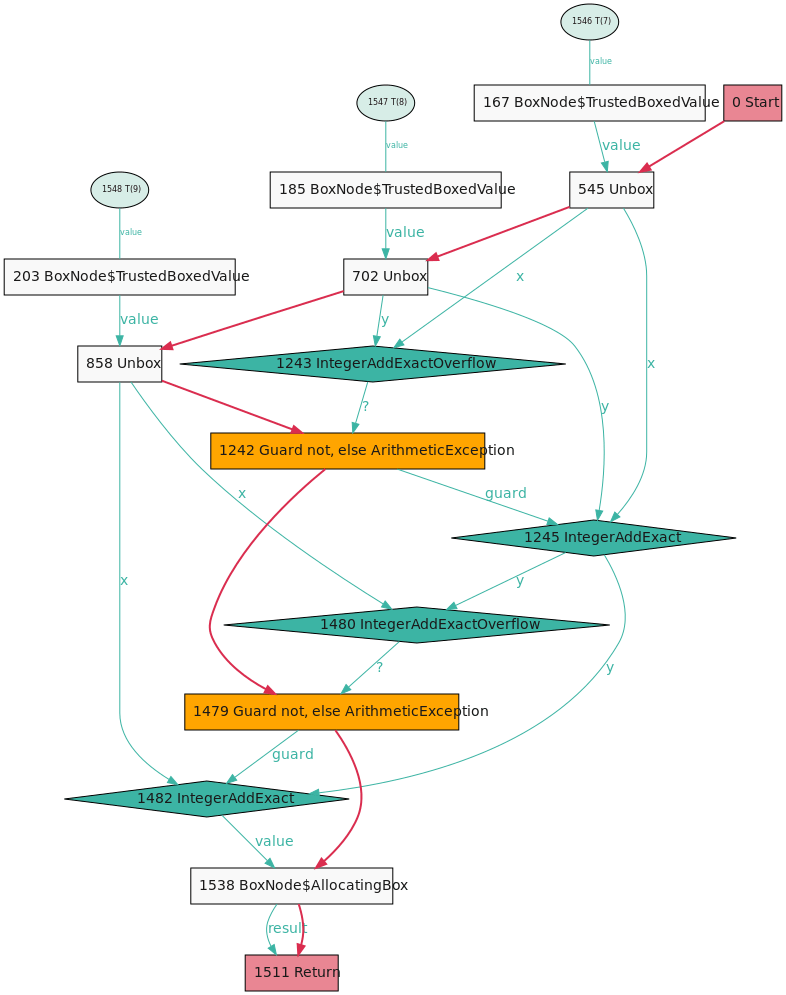
証明を与える方法のひとつは、単に&演算を用いることです。3つの値をビットマスクして1バイトの範囲に収まるようにする形でaddを変更すれば、それによって演算がオーバーフローする可能性がないことを証明できます。

def add_masks(a, b, c)
  a &= 0xff
  b &= 0xff
  c &= 0xff
  a + b + c
end

これでExactノードがグラフから消え去り、代わりにずっとシンプルな基本の+ノードになりました。これがどのようにして起きたかを観察できます。そこに流れ込むスタンプは、それらの値が十分小さく、オーバーフローする可能性がないことを示しています。2つ目の+には[0 - 510]になるスタンプが入力され、出力には[0 - 765]になるスタンプがある点にご注目ください。

対応するマシン語コードは以下のようになります。

    0x1211f4095:    and esi, 0xff
    0x1211f409b:    and r10d, 0xff
    0x1211f40a2:    and eax, 0xff
    0x1211f40a8:    add r10d, eax
    0x1211f40ab:    add r10d, esi

これこそが本来のねらいです。つまり、値の範囲を証明するビットマスクを追加して、演算がオーバーフローしないことを証明すれば、優秀なコンパイラがその情報を活用してオーバーフローチェックを除去してくれるということです。

ここで、スタンプ付きの値はローカル変数に保存されており、それを取り出したものを利用している点にご注意ください。スタンプは保存から取得までの間存在し続けますが、それは問題ではありません。

スタンプの追加を組み込む

しかしビットマスクを導入すると、マスク命令が実際に実行されてしまうのが問題です。つまり余分なand命令が生じてしまいます。私たちは（プログラマとしての推論によって）実際には値が範囲内に収まることを知っているので、このand命令は何も行っていないに等しい無意味な存在です。私たちはコンパイラにそのことを伝えていただけです。誤りである場合のリスクを承知のうえで値が範囲内に収まることを確信できるなら、もっとよい方法はないものでしょうか？

そこで、実際には何の操作も行わず、単にスタンプを「注入」する特殊な関数を書く手があります。私はこれをGraalおよびTruffleRubyでTruffle::Graal.inject_stamp(value, 0xff)として実装しました。この実装はコンパイラ組み込み（compilier intrinsic）です。つまり、コンパイラで認識され、異なる扱いを受けるメソッドということです。以下はGraalでの実装です。

r.register2("injectStamp", int.class, int.class, new InvocationPlugin() {
    @Override
    public boolean inlineOnly() {
        return true;
    }

    @Override
    public boolean apply(GraphBuilderContext b, ResolvedJavaMethod targetMethod, Receiver receiver, ValueNode value, ValueNode stamp) {
        b.addPush(JavaKind.Boolean, new InjectStampNode(value, stamp));
        return true;
    }
});

これは、コンパイラがinjectStamp呼び出しを見つけたら、代わりに上のコードを実行するというものです。このコードはグラフに特殊なInjectStampNodeを追加します。このノードはグラフ上にまったく出現しませんが、自分自身を単純化する最適化を行います。

public void simplify(SimplifierTool tool) {
    if (!hasUsages()) {
        return;
    }
    if (stamp.isConstant()) {
        int stampValue = stamp.asJavaConstant().asInt();
        replaceAtUsagesAndDelete(graph().addOrUnique(
            new PiNode(value, StampFactory.forInteger(32, 0, stampValue))));
    }
}

simplify演算では、スタンプの値（ビットマスク）を取得し、スタンプを追加するためだけの「πノード」と呼ばれるノードを用いてそれを注入します。実際にスタンプを探索するのはオーバーフロー演算であることを思い出しましょう。ここでは、スタンプがオーバーフローを許可しているかどうかをチェックしていることがわかります。オーバーフローが許可されていない場合は、自分自身をブーリアン定数falseに置き換え、決してオーバーフローしないことをこの値で示します。

public ValueNode canonical(CanonicalizerTool tool, ValueNode forX, ValueNode forY) {
    if (forX.isConstant() && !forY.isConstant()) {
        return new IntegerAddExactOverflowNode(forY, forX).canonical(tool);
    }
    if (forX.isConstant() && forY.isConstant()) {
        return canonicalXYconstant(forX, forY);
    } else if (forY.isConstant()) {
        long c = forY.asJavaConstant().asLong();
        if (c == 0) {
            return LogicConstantNode.forBoolean(false);
        }
    }
    if (!IntegerStamp.addCanOverflow((IntegerStamp) forX.stamp(NodeView.DEFAULT), (IntegerStamp) forY.stamp(NodeView.DEFAULT))) {
        return LogicConstantNode.forBoolean(false);
    }
    return this;
}

この「コンパイラ組み込み」を備えたaddは以下のようになります。

def add_stamps(a, b, c)
  a = Truffle::Graal.inject_stamp(a, 0xff)
  b = Truffle::Graal.inject_stamp(b, 0xff)
  c = Truffle::Graal.inject_stamp(c, 0xff)
  a + b + c
end

これで、グラフから&演算が消え去ってさらにシンプルになったことがわかります。この動的なRubyコードは、静的なJavaコードとほぼ変わらないぐらいシンプルに見えます。

そしてマシン語コードはというと、ご覧ください！マシン語のadd命令がたった2つになり、and命令は消え去りました。途中にmov命令が残っているのは惜しい点ですが、これはレジスタ割り当ての決定に基づいたものです。ハードウェアレジスタ名の変更によって、このコード例の途中に小さなしこりが残ってしまった点を除けば、実質的に何の違いもありません。

    0x12457278d:    add eax, dword ptr [r10*8 + 0xc]
    0x124572795:    mov r10d, eax
    0x124572798:    add r10d, esi

コードの予測が外れて、誤っている可能性のあるスタンプが注入されていたとしたらどうなるでしょうか。

誤ったスタンプを注入するプログラムを意図的に書いてみれば、オーバーフローや丸めが発生することを観察できます。このプログラムでは、最初の10秒間は正しく適用可能なスタンプを注入し、以後は範囲から外れた値が渡されるようになります。しかし、マシン語は既にオーバーフローチェックを行わない形で最適化されているので、下から2行目で例外が発生します。この値は丸められており、オーバーフローチェックが存在しないので、値はマイナスになります。

def foo(a, b)
  a = Truffle::Graal.inject_stamp(a, 0xff)
  b = Truffle::Graal.inject_stamp(b, 0xff)
  a + b
end

start = Time.now

until Time.now - start > 10
  a = rand(0xff)
  b = rand(0xff)
  raise if foo(a, b) < 0
end

puts 'state change'

loop do
  a = 0x7FFFFFFF
  b = 0x7FFFFFFF
  raise if foo(a, b) < 0
end

影響を測定する

さて、これは実際に有用なのでしょうか

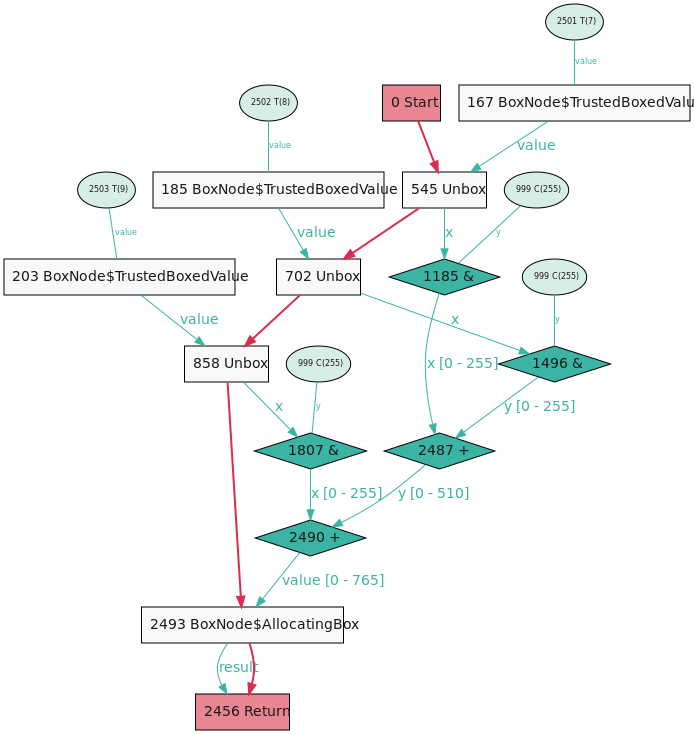
以下のコードは、RubyのグラフィックライブラリChunkyPNGから引用したものを少し簡略化してあります。これは透明度（transparency）の値に応じて2つの色を合成します。これらの色は「packed RGB」値として保存され、色の合成にはいくつかの整数演算が必要です。

def r(value)
  (value & 0x00ff0000) >> 16
end

def g(value)
  (value & 0x0000ff00) >> 8
end

def b(value)
  value & 0x000000ff
end

def rgb(r, g, b)
  r << 16 | g << 8 | b
end

def int8_mult(a, b)
  t = a * b + 0x80
  ((t >> 8) + t) >> 8
end

def interpolate_quick(fg, bg, alpha)
  alpha_com = 255 - alpha
  new_r = int8_mult(alpha, r(fg)) + int8_mult(alpha_com, r(bg))
  new_g = int8_mult(alpha, g(fg)) + int8_mult(alpha_com, g(bg))
  new_b = int8_mult(alpha, b(fg)) + int8_mult(alpha_com, b(bg))
  rgb(new_r, new_g, new_b)
end

このバージョンのグラフとマシン語コードを見てみると、大量のオーバーフローチェックがあるのがわかります。

...
    0x120f8329e:    sub esi, eax
    0x120f832a0:    jo  0x120f835fc
    0x120f832a6:    mov r10d, dword ptr [r11 + 0x2c]
    0x120f832aa:    mov r10d, dword ptr [r10*8 + 0xc]
    0x120f832b2:    mov edx, r10d
    0x120f832b5:    and edx, 0xff0000
    0x120f832bb:    shr edx, 0x10
    0x120f832be:    imul    edx, eax
    0x120f832c1:    jo  0x120f835b8
    0x120f832c7:    add edx, 0x80
    0x120f832cd:    jo  0x120f83612
    0x120f832d3:    mov r8d, edx
    0x120f832d6:    sar r8d, 8
    0x120f832da:    mov r9d, r8d
    0x120f832dd:    add r9d, edx
    0x120f832e0:    jo  0x120f835c5
    0x120f832e6:    mov r9d, r10d
    0x120f832e9:    and r9d, 0xff00
    0x120f832f0:    shr r9d, 8
    0x120f832f4:    mov ecx, r9d
    0x120f832f7:    imul    ecx, eax
    0x120f832fa:    nop word ptr [rax + rax]
    0x120f83300:    jo  0x120f835ad
    0x120f83306:    imul    r9d, eax
    0x120f8330a:    add r9d, 0x80
    0x120f83311:    jo  0x120f8351c
    0x120f83317:    mov ecx, r9d
    0x120f8331a:    sar ecx, 8
    0x120f8331d:    mov ebx, ecx
    0x120f8331f:    add ebx, r9d
...

しかしピクセル値が1バイトの範囲を超えないことはわかりきっているので、これらのチェックはことごとく無駄であることがわかります。ここにたった1行のコードを追加するだけでこの問題をきれいサッパリ解決できるのです！

まず、すべての値がランダムである画像をいくつか合成する作業をベンチマーク化します。

a, b, c = [], [], []

1_000.times do
  a.push rgb(rand(255), rand(255), rand(255))
  b.push rgb(rand(255), rand(255), rand(255))
  c.push rgb(rand(255), rand(255), rand(255))
end

Benchmark.ips do |ips|
  ips.report('interpolate_quick') do
    alpha = rand(255)
    a.size.times do |n|
      c[n] = interpolate_quick(a[n], b[n], alpha)
    end
  end
end

ここから1062バイトのマシン語コードが生成されます。

それではビットマスクをかけてみましょう。alphaを1バイトの範囲に収めるビットマスクをかけるコードをたった1行追加するだけです。

def interpolate_quick(fg, bg, alpha)
  alpha &= 0xff
  alpha_com = 255 - alpha
  new_r = int8_mult(alpha, r(fg)) + int8_mult(alpha_com, r(bg))
  new_g = int8_mult(alpha, g(fg)) + int8_mult(alpha_com, g(bg))
  new_b = int8_mult(alpha, b(fg)) + int8_mult(alpha_com, b(bg))
  rgb(new_r, new_g, new_b)
end

ここで生成されるグラフはずっとシンプルになり、マシン語コードは640バイトになりました。オーバーフローのノードもjo命令も消え去ったのに、ちゃんと動作します。つまり、このコードにあったオーバーフローのコストは完全に一掃されたのです。

...
    0x124f5a3b9:    and edx, 0xff0000     # the mask
...
    0x124f5a3df:    sub edx, r10d
    0x124f5a3e2:    mov r9d, esi
    0x124f5a3e5:    and r9d, 0xff0000
    0x124f5a3ec:    shr r9d, 0x10
    0x124f5a3f0:    imul    r9d, edx
    0x124f5a3f4:    lea r9d, [r9 + 0x80]
    0x124f5a3fb:    mov ecx, r9d
    0x124f5a3fe:    shr ecx, 8
    0x124f5a401:    add ecx, r9d
    0x124f5a404:    shr ecx, 8
    0x124f5a407:    add r8d, ecx
    0x124f5a40a:    shl r8d, 0x10
    0x124f5a40e:    mov r9d, eax
    0x124f5a411:    and r9d, 0xff00
    0x124f5a418:    shr r9d, 8
    0x124f5a41c:    imul    r9d, r10d
    0x124f5a420:    lea r9d, [r9 + 0x80]
    0x124f5a427:    mov ecx, r9d
    0x124f5a42a:    shr ecx, 8
    0x124f5a42d:    add ecx, r9d
...

今度は例の組み込みを試してみましょう。

def interpolate_quick(fg, bg, alpha)
  alpha = Truffle::Graal.inject_stamp(alpha, 0xff)
  alpha_com = 255 - alpha
  new_r = int8_mult(alpha, r(fg)) + int8_mult(alpha_com, r(bg))
  new_g = int8_mult(alpha, g(fg)) + int8_mult(alpha_com, g(bg))
  new_b = int8_mult(alpha, b(fg)) + int8_mult(alpha_com, b(bg))
  rgb(new_r, new_g, new_b)
end

生成されたマシン語コードは614バイトで、元のコードの60%未満です。ビットマスクand命令がなくなったので、さらにコンパクトになりました。

このマシン語コードは元のコードよりずっとコンパクトかつ素直で、大きく改善されているように見えます。しかし実際の実行時間には影響するでしょうか？

答えはイエスです。ビットマスクを使うと倍近く高速になります。しかもこれは純粋なRubyコードを1行追加しただけなのです。組み込み（inject_stamp）の場合もほとんど遅くならず、すべて誤差の範囲です。

おや、先ほどの「jo命令は大して遅くならない」という話はどうなったのでしょうか。私はこれまでずっとそう教わってきましたが、どうやらこの点をもう一度見直してもう少し測定してみるべきかもしれません。また、線形のオーバーフローチェックを除去すると一般にグラフ全体が和らぐので、おそらくスケジューリングも改善されるでしょう。これについても測定できればと思います。

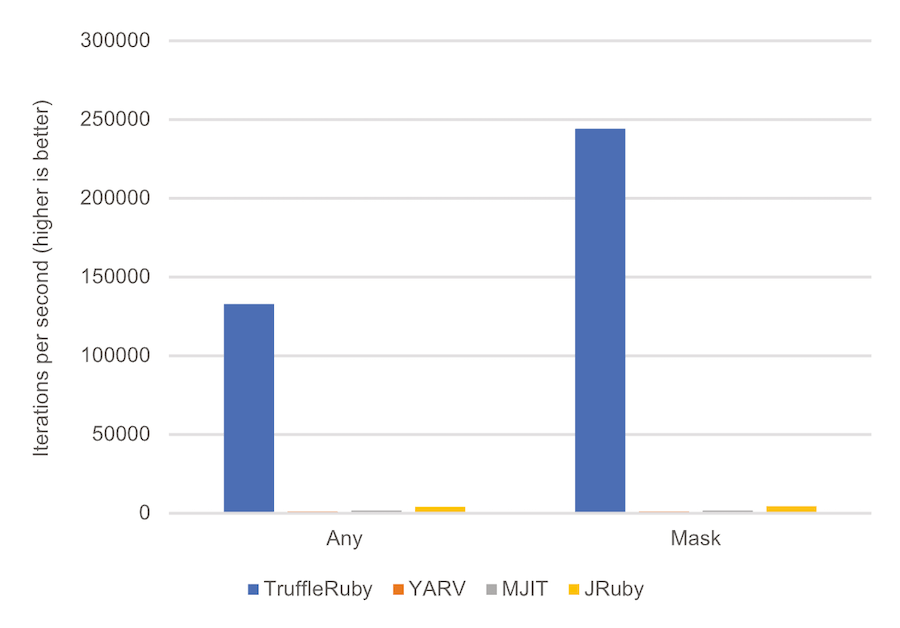
純粋なお楽しみとして、洗練されたスタンプシステムを備えたTruffleRubyをMRIやその他の最適化済みRuby実装と比較してみましょう。

このベンチマークでは、ビットマスクは他のシンプルな実装では効果が目立ちませんが、TruffleRubyはYARVの200倍高速、MJITの140倍高速、JRubyの50倍高速です。

それではまとめに入りましょう。純粋なRubyで算術演算がオーバーフローしないことをコンパイラにヒントとして伝える方法はたしかに存在します。やるべきことは、コンパイラが利用できる形で証明を書くことだけです。本物のRubyコンパイラならその証明を利用できます（他のコンパイラも利用できるはずです）。これは実際にパフォーマンスに有益な影響をもたらします。

asm.jsにも関連している

値を& 0xffでビットマスクするというアイデアにどこかで見覚えがありませんか。asm.jsはJavaScriptのサブセットで、本記事でやっているのと同じ要領でより多くのハードウェアプリミティブを用いて効率を高める設計になっています。Asm.jsサブセットでは、value | 0というパターンを用いて値を強制的にマシン語整数として扱います。

関連記事

Rubyオブジェクトの未来をつくる「シェイプ」とは（翻訳）