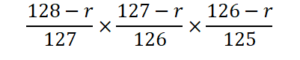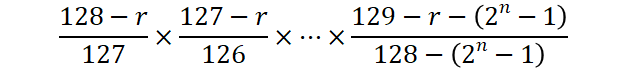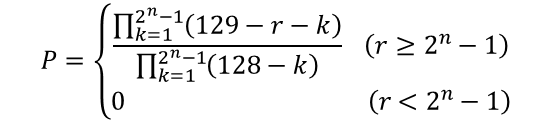こんにちは、ゲームと確率が大好きなnozueです。
ポケモンピカブイ発売されましたね!!
初代をたくさんプレイした私にとってはとても嬉しいです。今回はポケモンをボールから出して一緒に連れて歩けるので、好きなギャラドスを出してみたのですが、水の中でしか連れて歩けなかったです・・・残念(´・ω・`)
さて、私が今やってるソシャゲで、この前ギルド対抗のトーナメント(以下、トナメと略します)が開催されました。
確率が大好きな私は、どうしても何回戦まで勝てるかというのを知りたくなり、求めるに至りました。
求めた後に気づいたのですが、やはり同じように考えている方がいました。
前提条件とか考え方が結構似てて、みんな考えることは一緒なのかなあと思いました。
この記事と違うのは以下の点です。
- 変数の置き方、結果式
- 違ったアプローチ
- (本記事は)具体例を入れてある
途中経過はいらないよ!結果はよはよ!って方はこちら(ページ内リンク)
それでは以下、説明です。
注意
- 高校数学レベルの確率の知識がある前提で話しています。
なるべく分かりやすく話しているつもりですが、知識が乏しい方にとって難しめの説明となるのはご了承ください。
前提条件
- シードが存在しない、参加者が2のなんとか乗(人)のトナメを考えます。シードを考えると複雑になるためです。
- 試合して勝敗を決めるために何らかの指標が必要です。仮想順位というものを各参加者に設定し、仮想順位を比較して上位の参加者が必ず勝つものとします。
本記事特有の前提条件
数学の議論をする上では不要かもしれませんが、本記事で分かりやすく説明する上で必要な条件になります。
- 参加者は128人(2^7人)とします。
途中式を見た時に参加人数だとすぐわかるようにするため、ある程度大きな値にします。例えば、127という数字は、参加人数-1を表しているだろうと簡単に推測することができます。 - 自分を一番左の位置に配置します。今回求めるのはn回戦まで勝ち抜ける確率であり、n回戦内での対戦順には意味がないため、左に持ってきても等価なトナメとなります。
- 参加者の配置について。自分を一番左に配置した後に、自分に近い部分から参加者を1人ずつ配置していきます。
考え方
求めるもの
参加者128人のトーナメントで、仮想順位rの参加者がn回戦を勝ち抜ける確率
です。n回戦を勝ち抜ける確率であって、n回戦まで勝ってn+1回戦で負ける確率ではないということです。
以下、n=1のとき、n=2のときを求め、そこから一般化していきます。
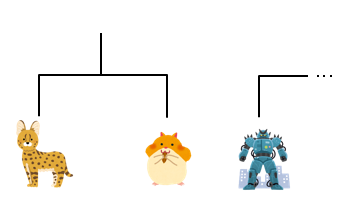
n=1のとき
対戦相手が自分より弱ければ良いです。2回戦以降の相手のことは気にしなくてよいため、それ以外の参加者には気にする必要がありません。
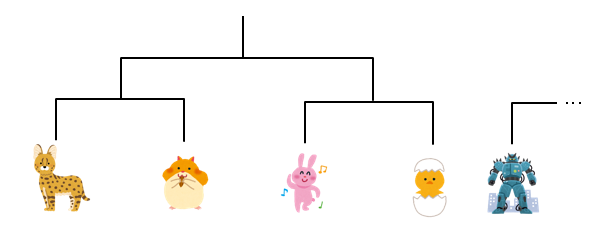
n=2のとき
2回勝ち抜けた時、負けた3人が自分より弱ければ良いです。
1人目を配置した前提で2人目そして3人目を配置すると考えれば、1人目を配置する確率、2人目を配置する確率、3人目を配置する確率を掛けたものとなります。
1人目が自分より弱い確率というのは先ほどと同様です。
2人目の確率は、1人目よりも、自分より弱い参加者の数、全参加者の数 が1ずつ減っています。この確率は
(127-r)/126
です。3人目も同様に考えます。
となります。
nのとき
n=1,2のときと同様に考えて、負けたX人全員が自分より弱ければ良いです。
Xには何が入るでしょうか?
n=1のとき、X=1
n=2のとき、X=3
…
nのとき、X=2^n-1
となります。求める確率は、
となります。
隠れた条件?
ここまで求めた段階で、おかしなことに気づいた方がいるかもしれません。
この式を見ていると、どんな順位の人でも1日目、2日目…n日目に勝つ確率が少なからずあるように見えるということです。
例を挙げて考えてみましょう。仮想順位128位の人は絶対に1回戦を勝ち抜けられません。127位の人は、1回戦で128位の参加者と当たった時のみ勝てますが、2回戦は必ず格上と当たるため、絶対に勝てません。
色々と考えた結果、回戦ごとにボーダーの順位があると考えに至りました。言い換えると、n回戦ではボーダーrが存在し、一定以上のrでないと勝てないという条件です。rがボーダーより低い場合は勝ち抜ける確率は0となります。
n回戦でのボーダーを調べてみると、
n=1のとき、r=127 (自分より下に1人いれば良い)
n=2のとき、r=125 (自分より下に3人いれば良い)
…
nのとき、r=128-X (自分より下にX人いれば良い)
という条件になります。このXは先ほどのnのときと同じで、2^n-1となります。
結果
参加者128人のトーナメントで、仮想順位rの参加者がn回戦を勝ち抜ける確率Pは
となります。Π(パイ)は総積と言って、全て掛けたものです。Σ(シグマ)は高校でも習いますが、Πは普段見かけないものかもしれません。2行目の0 (r < 2^n-1)は分かりやすさのために書いてあります。r < 2^n-1のときでも、1行目の式に当てはめればP=0となります。
この式だけでは全然想像がつかないと思いますので、rやnに具体的な数字を入れてグラフにしてみたいと思います。
グラフ
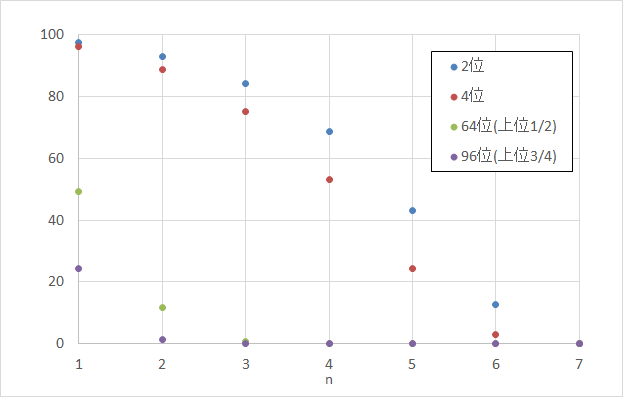
128人のトーナメントで仮想順位2位、4位、64位、94位の参加者がn回戦まで勝つ確率です。
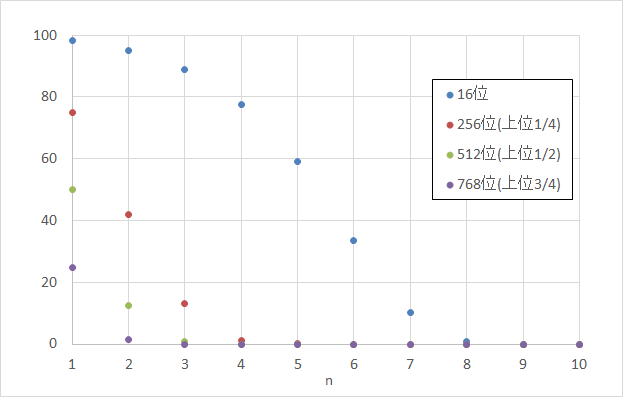
続いて、参加者を増やしてみます。
1024人のトーナメントで仮想順位16位、256位、512位、768位の参加者がn回戦まで勝つ確率です。
1回戦については自分が上位どれくらいの位置にいるかがそのまま勝つ確率になるように見えます(例えば、上位1/2なら勝率1/2)。
2回戦以降は、よほど上位でない限り、急激に下がる。ということが分かります。
おわりに
実際のトナメでは本番に強い人、格上相手だとやる気になって力が何倍にもなる人がいたりするため、今回求めた確率がそのまま当てはまるとは限りません(もしかしたら、これらの参加者の性質を考慮して仮想順位を設定すればより正確になるかもしれません)。参考程度に留めておいた方が良いとは思います。
私のやってるソシャゲでは、4人バトルロイヤル2人勝ち抜け方式でした。これは、同時に4ギルドで争って、2ギルドが勝ち抜けるというものです。ページの長さの都合上、今回は触れませんでした。反響があれば、またの機会に書きたいです!!