こんにちは、 ebi です。
突然ですが、僕は趣味でビリヤード(キャロム、スヌーカーではなくポケット)をダラダラ続けてはいるのですが、どうにも不真面目でまともにセオリーや理論を学ぼうともしません。これじゃいかん、と言うことで今回は独自に理論的に計算したり何かしらを作ってみたりしながら、ビリヤードのシステムを取り上げつつ学んでみます。
仕事にも通じるけど、自ら色々と考えたり、手を動かしてみれば覚えるじゃろ。の精神です。
なお、本記事中ではあくまでざっくりとした理論と要点だけで進めちゃうのと、中・高校生レベルの数学や物理、ビリヤードのルールとか雰囲気とかはある程度分かっている前提で書いていきますので、諸々の説明が不足している点はご了承ください。
駆け足で書いたので普通に間違ったこと書いてあったりしたらごめんなさい。
最近のご時世のせいか、土方隼斗プロや大井直幸プロを始めとする国内トップのビリヤードプロの方々が YouTube チャンネルで色々な動画を上げてたりもします。
ビリヤードに少しでも興味がある方は、この記事を読んだ後でも前でも是非その辺もご覧になってみてはいかがでしょうか。
最初に成果物披露
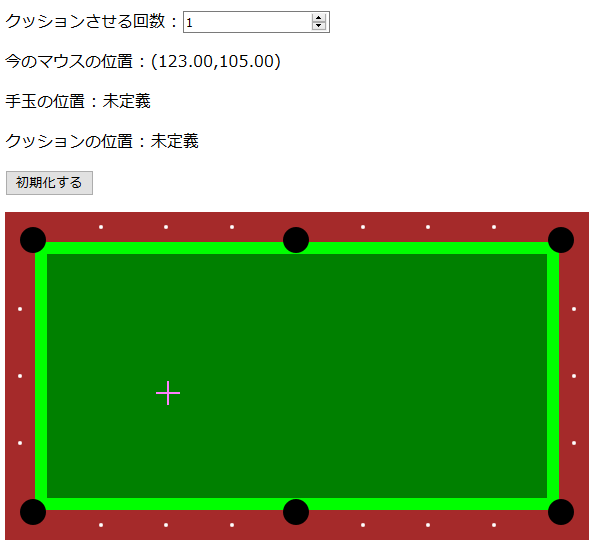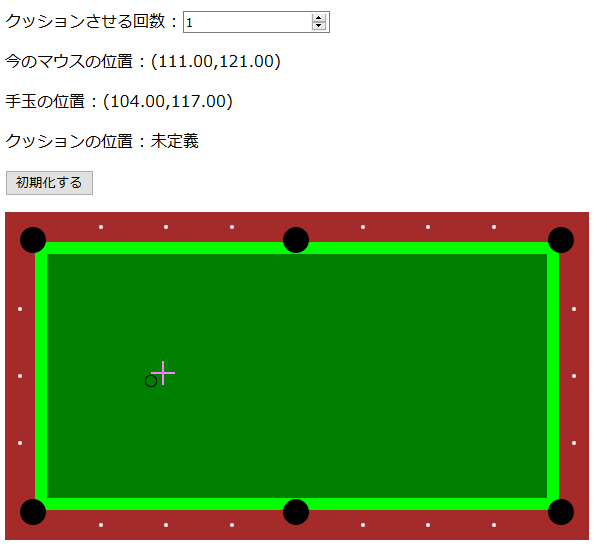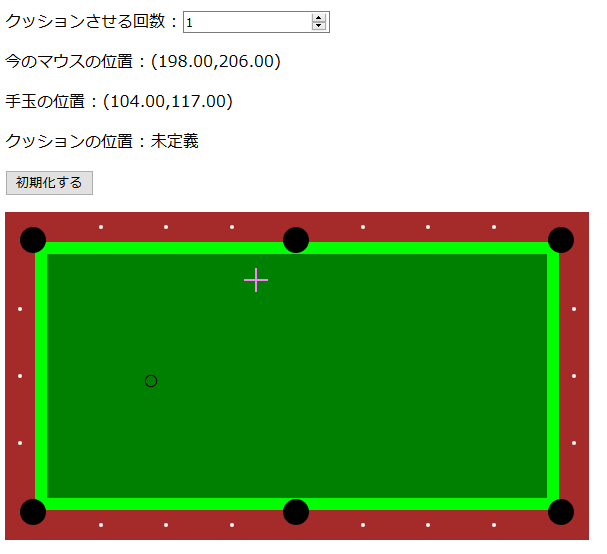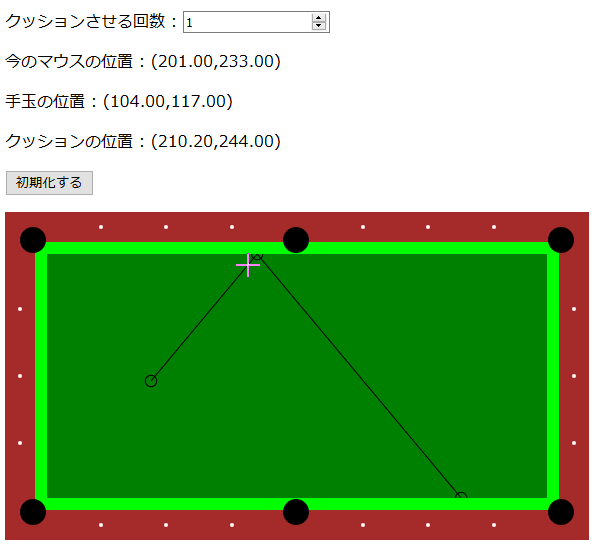
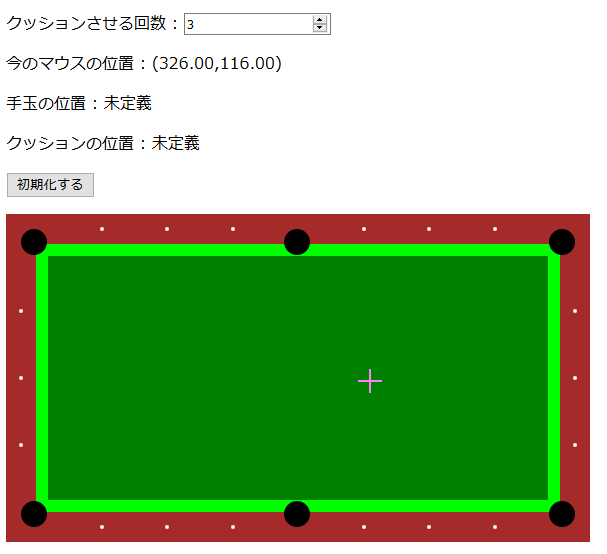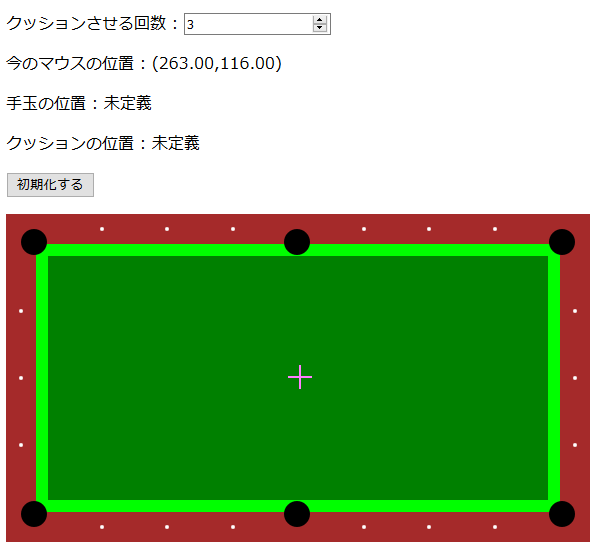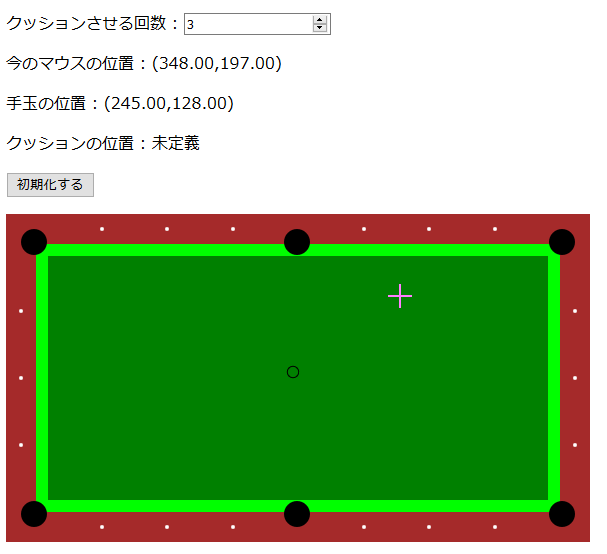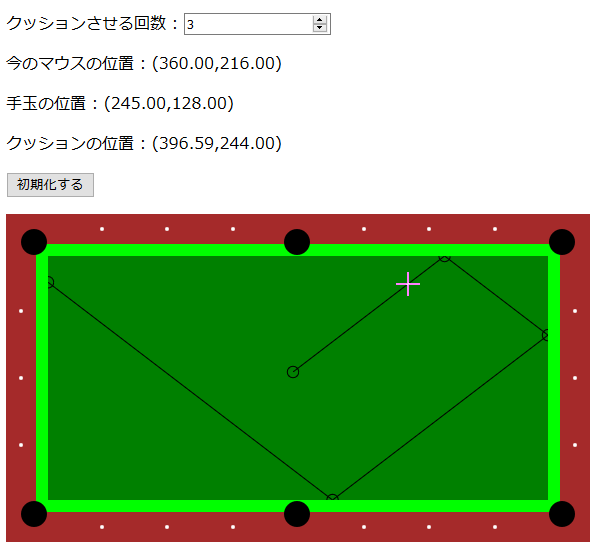
マウスカーソルで手玉の位置と最初のクッション位置を選べば、あとはビリヤード台もどきにそれっぽい反射軌道を描写してくれるシミュレータもどきを作りました(あくまでお遊びの範囲で作ったものなので厳密性はありません。予めご了承ください)。
このページで遊べますが、 PC 向けです。
理論編
手玉の動きを近似できそうな問題に落とし込む
まずは適当なビリヤード台と手玉(キューで突く白いボール)を仮定して、計算がしやすい超単純な物理法則をするボールの動きの公式を導き出してみます。
適当なボールの動きを想定して、こんな図を書いてみました。使い慣れてる draw.io で書いたのでお手製感満載の汚い図でごめんなさい……。
数学や物理の問題に出るような図ってどうやって書いたらいいか知らない……。
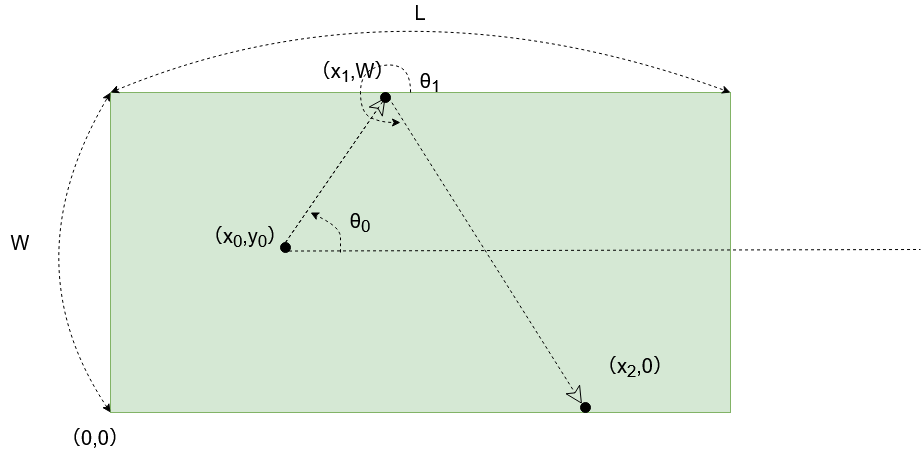
- ビリヤード台の横幅をL(ビリヤード用語としては、こっち側の方が長いので長クッション、逆側を短クッションと呼んだりする)、縦幅をWとします。
ビリヤード台の幅と言ってますが、正確に言うと実際の幅と言うよりは、手玉が動く領域になってきます。
あともちろん実際のビリヤード台には 6か所 ポケット(穴)があります。ポケットも書くと複雑なので割愛します。 - 左下の地点を(0,0)の基準点とします。
- 最初の手玉の位置は(x0, y0)から始まり θ0 の角度に動き出します。
- 手玉は長クッションに当たり、反射すると(x1,W)の位置から θ1 の角度に動き出します。
当然、最初の手玉の位置や動き出す角度によっては、長クッションではなく、短クッションに入ることもありますがある程度そう動くだろうと予測がつく範囲でしかこの仮定を利用しないものとして無視します。 - 1クッションした手玉は(x2,0)の位置で2クッション目の反射をします。以下こう言う運動の繰り返しのはずです。
- 手玉とクッションの衝突の際は、摩擦力は働かず、完全弾性衝突をし、入射角と反射角が等しい動きをするものとします。
- 手玉に一切の回転はかかっていないものとします
手玉がクッションと衝突する地点を求める公式を導き出す
三角関数の知識を使えば一瞬ですね。
1回目の衝突位置については、
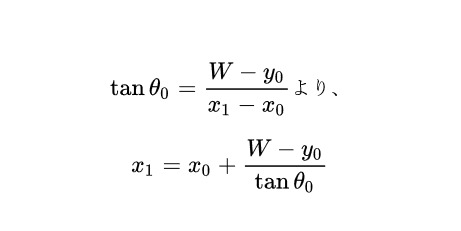
2回目の衝突位置については、
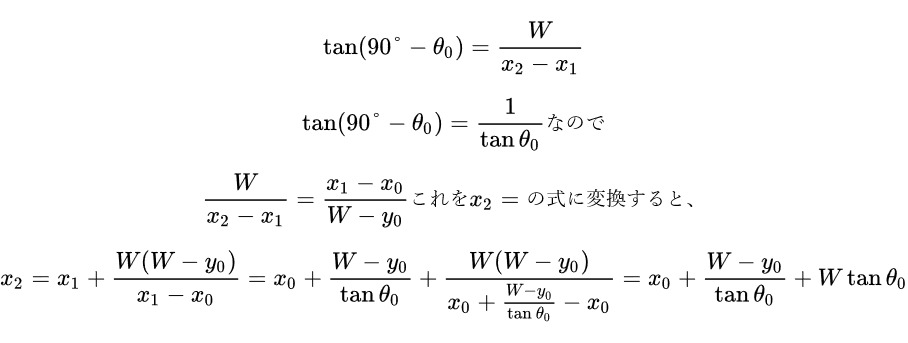
と言うことで、手玉が動く角度が分かっていると手玉がクッションする位置 x1 や x2 は分かります。
実際考えるときは、最初にクッションさせたい位置を決めることで逆算して手玉を動かす角度 θ0 が決まって、それにより2クッション目の位置が決まるので、それを自分のイメージコースと比較するかもです。
もうちょっと広く使えそうな公式にしておく
手玉がクッションする位置の候補は、こんな感じで 4種類に分けられそうですが、先ほどは勝手にここに来るだろうと予想して決めつけて計算してしまいました。もうちょっと汎用的なものに落とし込んでみましょう。
- 奥の長クッションに入る : (x1,W)
- 手前の長クッションに入る : (x1,0)
- 奥の短クッションに入る : (L,y1)
- 手前の短クッションに入る : (0,y1)
手玉が動ける範囲は限られているので、定義域として 0 ≦ x0 ≦ L , 0 ≦ y0 ≦ W があります。↑4つの仮定で式を解いてみて、この定義域範囲内に収まる回答があれば、一応それが正しいクッション位置にはなりそうです。
ボールの動く角度 θ0 によって、もう少し候補を分類できそうなのでやっておきます。
x軸方向の運動に着目します。奥の短クッションに入る動きは、 x 軸の正の方向への運動に絞れそうなので、 cosθ0 が正の値の範囲になりそうです。
つまり、 ![]() です。
です。
逆に手前の短クッションに入るときの条件は ![]() です。
です。
なお、 θ0 が 90° , 270° の時は完全に y 軸向きへの運動になります。なので短クッションに入ることはありませんので、 = は付けてません。と言うか直線に動くだけの運動は考えるまでもないので今回は無視しますね。
y軸も同様に考えると最終的にこんな感じになりそうです。

まだ解いていない残りのクッション位置の式も解いてまとめておきます。

所詮は直線で動く一次関数の動きをしているだけなので tanθ が傾きであることを理解していると、一気に楽になる問題だったりしますかね。
クッション後の手玉の移動方向
最初の例で取り上げたように、長クッションに入ったときは、y軸方向の動きが反転して、x軸方向の動きはそのままです。
言い方を変えると、cosθ は同じ。 sinθ が負の値になる角度になるので、角度としては 360°-θ になるってことです。
短クッションに入ったときは、逆の考え方でよくて、x軸方向の動きだけが反転するので、 sinθ は同じなんだけど cosθ が負の値になる角度を考える。これは 180°-θ になります。
長・短(短・長)の2クッションを考える時もよくありますが、2クッションしたあとの玉の動く方向は 180° -(360°-θ) = θ - 180° で丁度手玉を突いた方向と真逆の角度になっています。
まとめると、
- 長クッションに入ると反射角は 360°-θ (y軸方向の速度が逆になる)
- 短クッションに入ると反射角は 180°-θ (x軸方向の速度が逆になる)
- 長・短クッションに一回ずつ入ると、2クッション後の反射角は θ - 180° (x軸、y軸方向の速度がそれぞれ逆転して、最初に手玉が動く方向の真逆になっている)
入射角・反射角の証明
しれっと使っちゃってるんで、手玉とクッションが摩擦なしで衝突する前提の時に入射角と反射角が等しくなることも証明しておきます。
手玉の重さは m とします。手玉は v0 の速度で動いていたとします。反射後は v1 の速度で動きます。
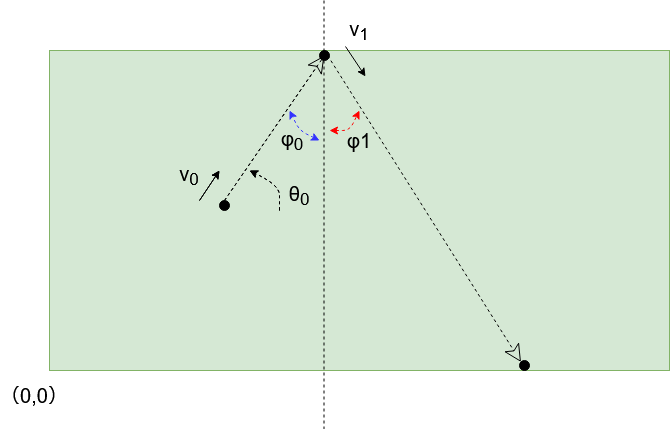
手玉とクッションは衝突をしているので、運動量保存の法則を使って、
![]()
が成り立ちます。手玉の重さ m は一緒なので v0 = v1 です。つまり速度が全く変わってません。なんか変な式ですね……。
このケース衝突対象がいないんですよね。手玉はクッションに当たります。クッション≒ビリヤード台でしょうか。ビリヤード台は超重いです。手玉を思い切りあてたところで動きはしないでしょう。
つまり衝突後のビリヤード台の速さ V1 も衝突前の静止しているビリヤード台 V0 も 0 なので無視されてると考えます(こんなすげー適当な話書いて誰かに怒られないか……?)。
さて、本題の入射角、反射角の話を使用したいので速度成分を x 軸と y 軸に分けてみます。
x 軸の速度は ![]()
x 軸で運動量保存則を考えると、
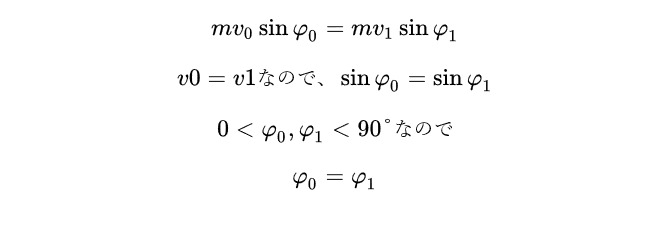
こんなつまらん証明問題ある……?
なんか間違ってる気がするけどまぁいいか……。手玉と的玉の衝突の話持ち出した方がよかったかな……。
クッションとの摩擦、手玉の速度と反射角の角度について補足
さて、実際は手玉とクッションの間で x 軸方向には摩擦力が働くのだと思う。摩擦力は進行を妨害する向きに働くので、 v0 >v1 になるでしょう。
すると、釣り合いを取るために sinφ0 < sinφ1 になるので、入射角に比べると反射角の角度が開くと考えられます。
また、手玉の速度が遅いとそれだけクッションと接する時間が長くなり、摩擦力がかかる時間は長くなるはずです。
つまり、 v1 の速度がそれだけ落ちると言うことなので、手玉が遅いほど反射角の角度は開いていく。と考えられます。
こんな感じでざっくりと手玉の速度とクッション反射の角度の違いも物理的に説明できました。
手玉を強く突くと入射角より反射角の方が小さくなる。みたいな話も見る気がするけど、それは手玉の回転やクッションの反発力を考慮した時でまた別の話ってことでいいんかな……。
クッションの反発力で y 軸方向の速度が加速されるなんてあるのか……?そしたら x 軸方向の速度が変わってなくてもベクトル的に反射角度が大きくなるのはあり得るのかな……? 🤔
まぁこまけぇこたぁいいんだよ!!(もっとまともな解説をする文献の紹介待ってます)
ビリヤード台などのスケールを調べておく
先ほどの式上では W や D と記載していた固定値や手玉の大きさなんかも忘れず調べておきましょう。
ポケットビリヤードに関するNBA(公益社団法人日本ビリヤード協会)ルールブックを見に行きます。
「第2章 器具」に規定が載ってましたので、これを抜粋してメモっておきます。
- ビリヤード台(第1条 ビリヤードテーブル 第2項より): クッション内径が、2540mm(100インチ)×1270mm(50インチ)
- ボール(第2条 ボール 第2項より) : 直径は56.5mm~57.2mmであり、重量は165g~175gのもの。
- サイドポケット(第1条 ビリヤードテーブルの添付図より) : 口径 135~145mm
- コーナーポケット(同図より):口径 125~135mm
同ルールブックより抜粋
実践編
理論編の内容を元に手玉の動きシミュレータっぽいものを作っていく
画面をポチポチやるようなものを想定するので使い慣れている HTML、CSS、JS あたりで作ります。
高々二次元の運動を考えているので特に凝った JS ライブラリは導入せずに Canvas を使うことにしました。動的に色々変えたいので Vue.js を使用します……。
できました

結構ここまでの内容を書くだけでも疲れてきたのでソースコードの解説とか作る流れは割愛しちゃいましたが、 GitHub に内容公開はしておきます。
脳直で書くだけ書いた初稿のまま放置されているので、あまり実用的なソースコードではないのはご容赦ください。
見切り発車で始めたせいもあって、さきほどの問題仮定と Canvas の座標定義のための y 軸方向が逆方向でちょっと困ったんですが、 Canvas を rotate させる CSS 適用させて乗り切る英断ができたのが一番のポイントでしたでしょうか。
細かい造形をサボっているせいで分かり辛い部分を補足をしておきます。
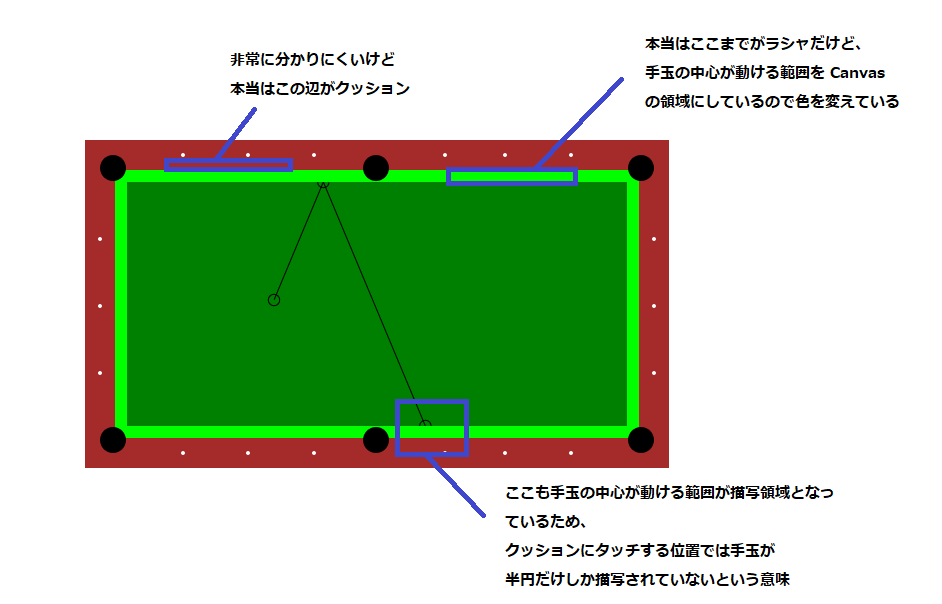
前説が長くなりましたが本題のシステム検証に入っていきましょう。
ハーフVシステムを検証してみる
ハーフVシステムは1クッションの単純な手玉の動きを公式で覚えるものです。
あとから細かい点は訂正していくのですが、ざっくり言うと
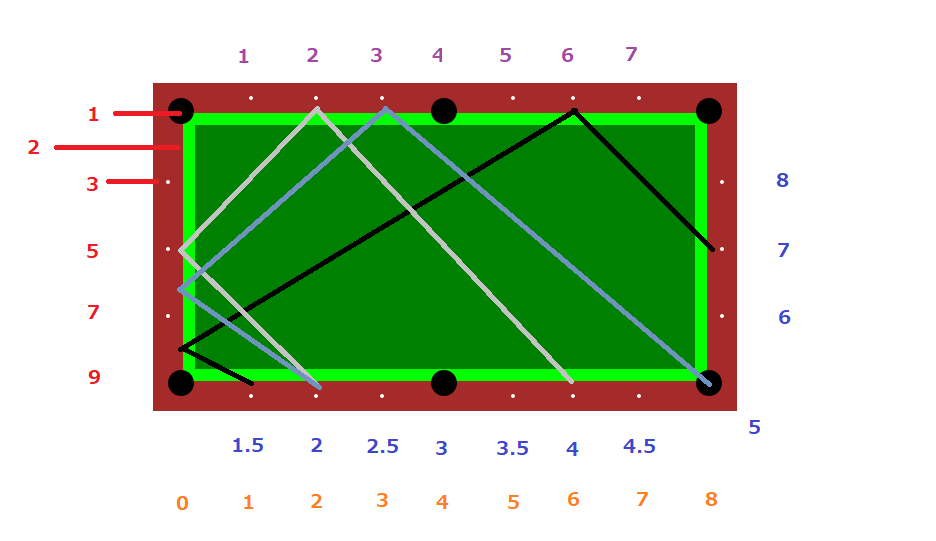
ビリヤード台のポイントを参考に、下記の図の 赤い数字 × 青い数字 = 紫の数字 になる位置を線で結ぶようにして手玉を突けばよい、と言う公式です。
例として 5 × 4 = 20 になる形で線を結んでいます。
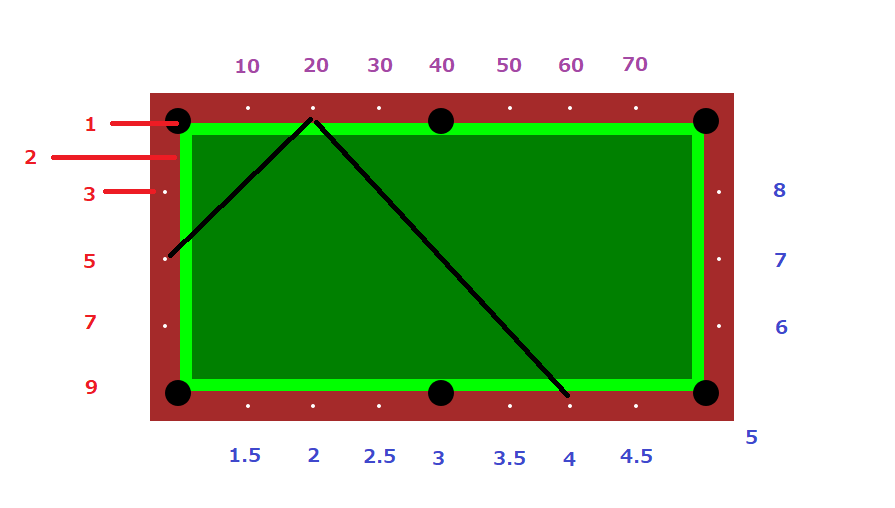
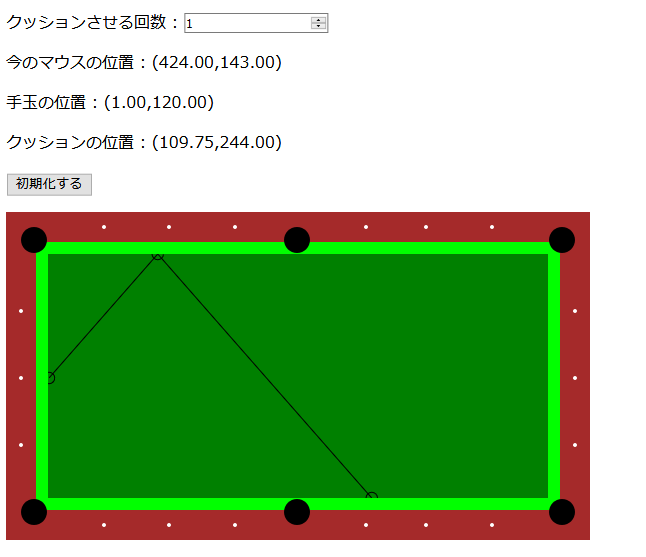
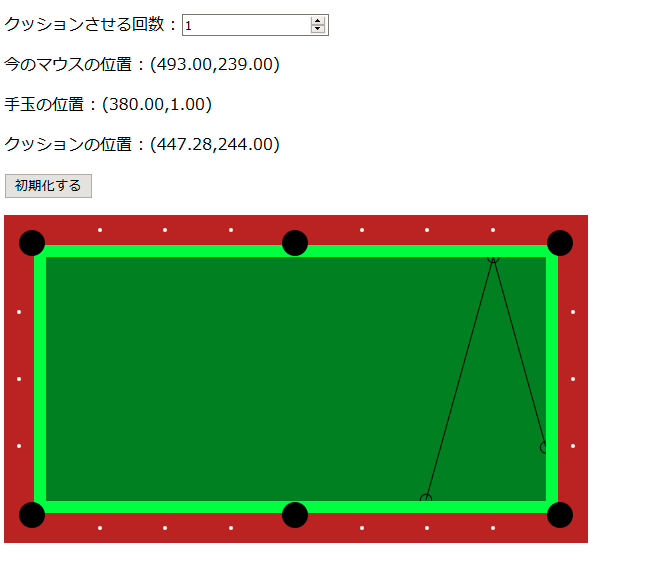
さて、適当にポチポチっと手玉の位置とクッションさせる位置クリックしてみます(伝わりにくいですが、手玉は左側の位置からスタートしてます)
うーん、なんかそれっぽいところに手玉が向かっている気がします!!
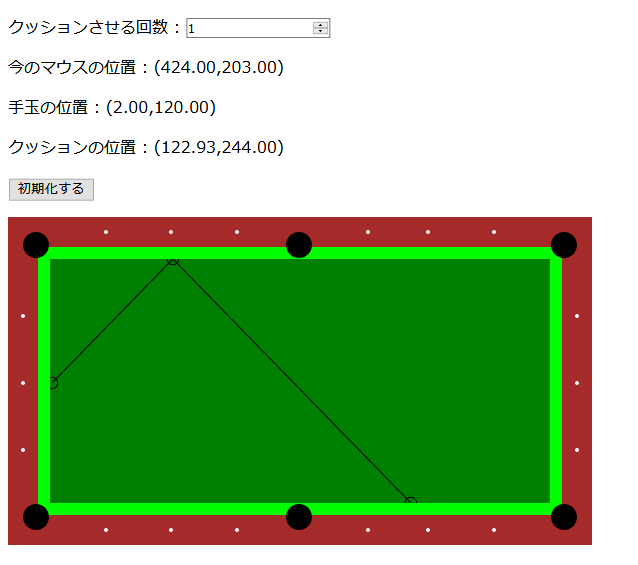
ただ、実際に狙うときってポイント自体を狙いにする方が断然楽でこのシステムも本当はそう狙えって言われます。
ポイントってクッションから少し距離ありますよね。すると手玉がクッションする位置ってさっきよりも手前になってきます。こんな感じでしょうか……。
あれぇ……結構手玉の位置が違くない? 😅
だから、実際はポイントを狙ったうえで更に順捻り(クッション後の角度が開く向き、この場合は右捻り)を入れる必要があるんですね!
こんな適当な話書いてて誰かに怒られないか?(2回目)
ファイブ&ハーフシステムを検証してみる
ファイブ&ハーフシステムは、さらに一段階難しくなって3クッションの動きを考えるものになります。
先ほどの図の紫の数字を 1/10 にして、対角の長クッションにも同じ間隔値でオレンジの数字を定義します。
今回は
青い数字 - オレンジの数字 = 紫の数字
が指標になってきます。
適当に3パターンくらい例の線を引いてみます。今回は最初からほんのりポイント狙いに寄せてみます。
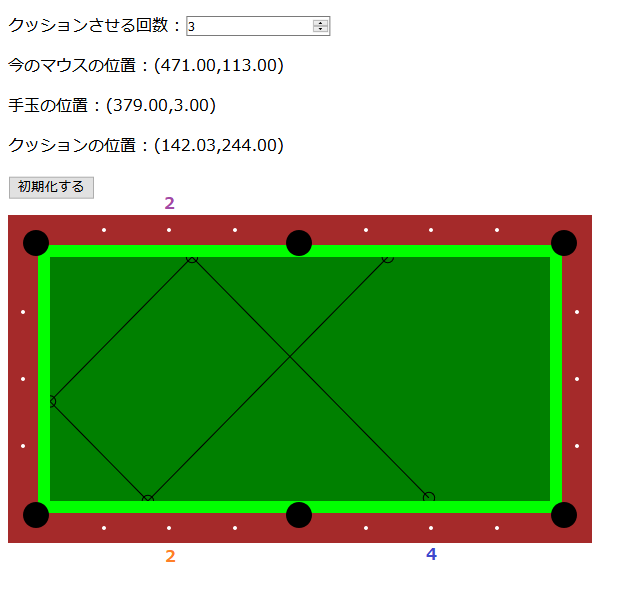
まずは灰色の線から。 4 - 2 = 2 。
順捻り入ればまぁまぁ狙い通り?(これまた伝わり辛いですが、以後手玉は全て右下に近い位置からスタートしてます)
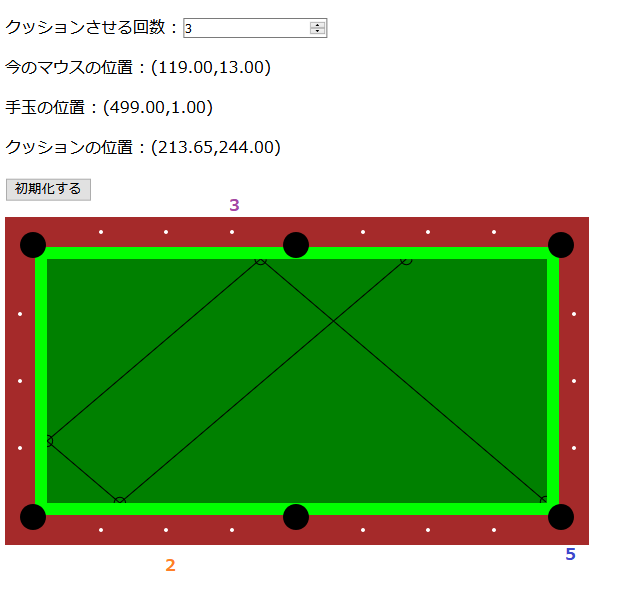
次にやや青っぽいグレーの線。 5 - 2 = 3 。
んん、隣のポイントの方が近くない……? 🤔
最後に黒の線。 7 - 1 = 6 。
うん、これは流石にやる前から気付いてたんだけど、理論的な角度からすると大分捻り入ってないと無理があるよね……
にわか知識しかないので、正直使い方を間違っていることを疑うレベル。
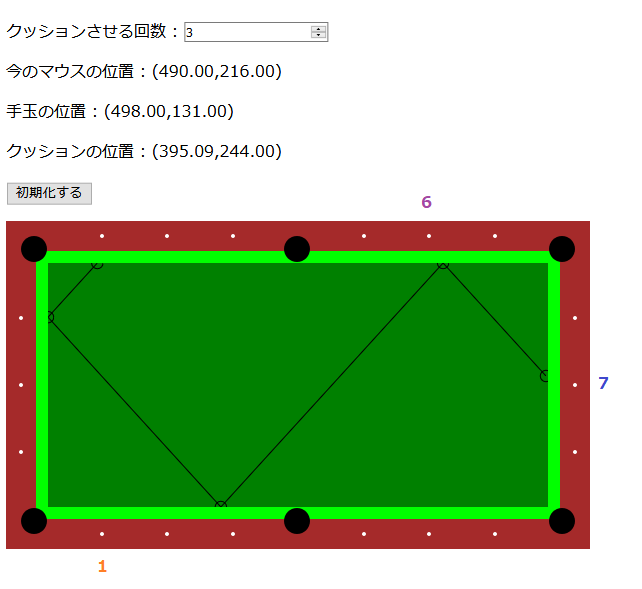
傾向からすると、手玉がなるべく対角線の位置にあるコーナーに近い軌道の方が狙いに近い軌道をなぞっている気がしました。
うーん、でも、それってそもそもボールが散乱する領域が限られている軌道だから適当に狙っても当たりやすいって話ではない……?
あるいはクッションに対して、平行な速度成分多めで入る場合の摩擦力の差を考慮しているとかあったりするんでしょうか。
くれぐれも勘違いしないでいただきたいのですが、あくまで本検証は大分現実と異なる世界での動きを想定していて、実際はクッションでの反射はこの通りにならず、摩擦で手玉も徐々に速度が落ちてきますし、順捻りも反映できていないので結果を真に受けすぎないでください。
ポイントの位置なんかもものすごく適当に置いてるだけなので、実物の台での動きと厳密に比較する上ではあまり当てにはなりません。
と、フォローしておきます。
補足 - ポイント基準のクッションイメージのありそうな勘違い
せっかく作ったので、こう言うイメージ持っちゃってるときっと狙いがズレるよって話をおまけで書いておきます。
ポイントとポイントを繋いで二等辺三角形を作って、上手いことその直線状に手玉を転がそうと考えてみます。
今回は構える際にポイントを目指してボールを突く、ではなくポイントの位置にクッションさせることをイメージします。
例えば、このイメージは大丈夫なんですが……
(テーブルの中央に縦4ポイント、横2ポイントを基準に二等辺三角形を作るイメージを持ってクッションさせる。分かりやすく中央を使ってしまったのでサイドポケットに落ちちゃうよ!と言うツッコミはなしで)
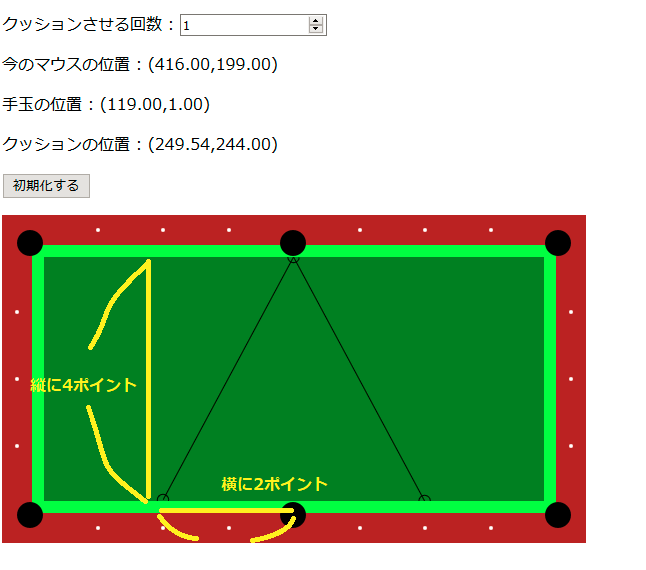
こう言うイメージを持ってしまうのは間違いです。
(同様に縦4ポイント、横3ポイントの二等辺三角形を作るイメージなんだけど、コーナー付近のポイントの間隔を利用して、コーナーに落ちるイメージを作る)
コーナーポケットに綺麗に入れるつもりで間のポイントを狙えたのに結構ズレちゃったなぁ 🤔
ってことが置きちゃう
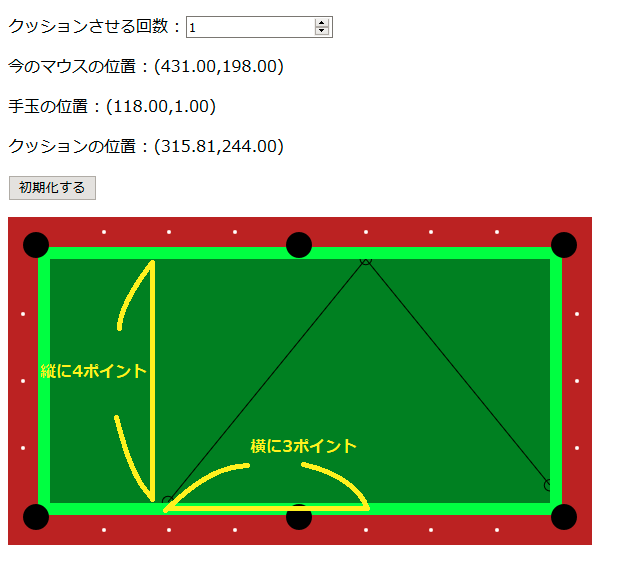
もう何回かクッションさせると分かりやすいですが、明らかに最初の狙い以外は綺麗なポイントの位置からズレています
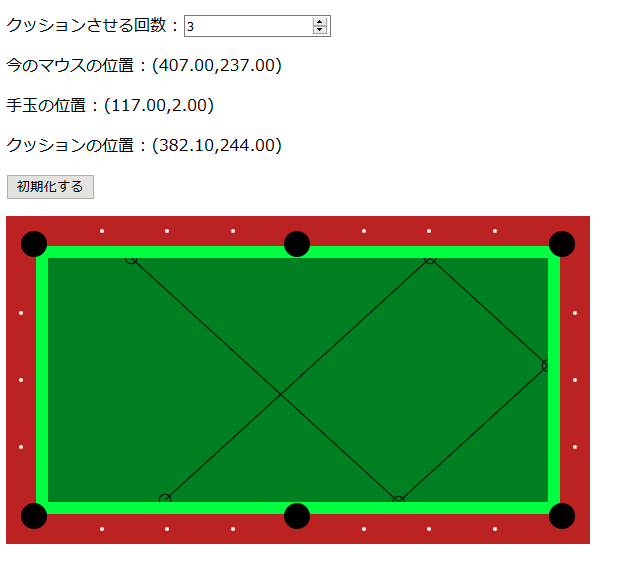
勘の良いひとはすぐ気付いていると思います。
確かにポイントは均等間隔で置かれていますが、最初と最後のポイントからコーナーポケット基準の 0 の位置を結ぶ間隔では、手玉が途中で当たってクッション反射が起きます(手玉の大きさがあるので、ラシャの端までは動けないのです)。
- 短クッションのポイントの間隔 : W/4
- コーナー付近で実際に手玉が動ける範囲の短クッションのポイントの間隔 : W/4 - r ( r は手玉の半径)
ってことですね。具体的に言うと先ほどの例では r tanθ だけ狙いとズレていたのでした。
傾きが急だとこんな感じで更に大きくズレて悲しいことになっちゃうので注意しましょう。
まとめ
と言うことで、中途半端な検証をしてみたことによって、ますますシステムの原理や信憑性がよく分からなくなりました。
それもそのはずでシステムはあくまでも基準となる目安を決めるものでしかなくて、それに合わせた捻り具合を自分で鍛えてくださいね、と言う程度のものだったりはするようです。
そもそも誰がどう言う基準でこれで狙いましょう!って考えたんでしょうね。
どこを狙うのか?だけでなくて何故そこを狙うのか?そこまで解説できそうな方がいたら教えを請いたいものです。
覚えるだけ覚えればクッションマスターになれるなんて甘い話はありませんでした……。それにしてももう少しズレに統一感がある公式にしてくれないものか?
クッションでの跳ね返り方や捻りのかかり具合なんかもそのお店、その日の台のコンディションにも左右されるでしょうし、結局は練習して経験あるのみですね……!!

