お久しぶりです。yoshiです。みなさん、夏を満喫していますか? 私は溶けそうです。日本の夏はとってもあつい。
覚えている方がいるかどうかは分かりませんが、以前私はRSA公開鍵暗号アルゴリズムを理解するという記事を書きました。今回はその続編(?)です。
楕円曲線について
楕円曲線、という言葉を事前知識無しで見ると、
多分こんな画像が脳裏に浮かぶと思います。違います。
楕円曲線の楕円は楕円積分から現れた言葉で、楕円積分は文字通り楕円の弧長などを求める方法なので全くの無関係とは言えませんが、少なくとも楕円曲線と楕円は別の図形です。楕円のことは忘れましょう。
実際の楕円曲線は、例を示すと以下のような曲線です。
 |
 |
一般化すると ![]() (ただし
(ただし ![]() または
または ![]() ) という式で表されるこのような曲線をワイエルシュトラス型楕円曲線と呼びます。ワイエルシュトラス型、と付いているのは他のパターンもあるからで、
) という式で表されるこのような曲線をワイエルシュトラス型楕円曲線と呼びます。ワイエルシュトラス型、と付いているのは他のパターンもあるからで、
 |
こんな形の楕円曲線もあります。こちらはモンゴメリ型楕円曲線と言い、一般式 ![]() (ただし
(ただし ![]() ) の形で表すことができます。
) の形で表すことができます。
いずれにしても、楕円曲線はx軸に対称の滑らかな曲線です。
楕円曲線上の点の加法群
楕円曲線上の任意の点の集合に、無限遠点 ![]() という特殊な点を加えることで、楕円曲線上の加法演算を定義することができます。
という特殊な点を加えることで、楕円曲線上の加法演算を定義することができます。
ここで言う加法演算は、実数の加法とは異ります。実数の加法と同じく ![]() という記号が現れますが、似たような性質を持っているために同じ記号が使われているだけ、といった感じに捉えてください。
という記号が現れますが、似たような性質を持っているために同じ記号が使われているだけ、といった感じに捉えてください。
楕円曲線上の点の加法は、以下のように定義されます。
任意の点 ![]() に関して、
に関して、 ![]()
![]() 以外の2点
以外の2点 ![]() に関して、
に関して、 ![]() かつ
かつ ![]() のとき、
のとき、 ![]()
それ以外の場合、
![]() のとき、
のとき、![]() と
と ![]() を結ぶ直線を
を結ぶ直線を ![]() 、
、
![]() のとき、楕円曲線の
のとき、楕円曲線の ![]() 上の接線を
上の接線を ![]() とする。
とする。
![]() と楕円曲線の
と楕円曲線の ![]() と異なる交点を
と異なる交点を ![]() とし、
とし、 ![]() の
の ![]() 座標を反転した点を
座標を反転した点を ![]() とすると、
とすると、 ![]()
と、言葉だけで説明するといまいち良く分からないですね。というか無限遠点って何だ。
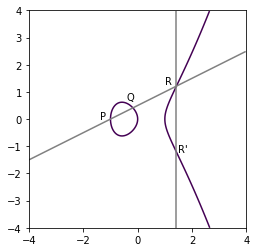
とりあえず無限遠点のことは置いといて、無限遠点じゃない点に関しての加法演算を視覚化してみます。
![]() と
と ![]() を通る直線と楕円曲線の新たな交点の
を通る直線と楕円曲線の新たな交点の ![]() 座標を反転した点
座標を反転した点 ![]() が一意に定まることが分かるでしょうか。
が一意に定まることが分かるでしょうか。
一方で、上図の ![]() と
と ![]() のように、x軸に対称な2点に加法演算を適用した場合、直線と楕円曲線は新たな交点を作らないので、楕円曲線上の一意な点を作れません。このような場合に解なしとしてしまうと加算群が作れなくなってしまうので、無限遠点が導入されます。
のように、x軸に対称な2点に加法演算を適用した場合、直線と楕円曲線は新たな交点を作らないので、楕円曲線上の一意な点を作れません。このような場合に解なしとしてしまうと加算群が作れなくなってしまうので、無限遠点が導入されます。
無限遠点について
無限遠点という概念を飲み込むのに引っかかりを覚えてしまう人は少なくないかと思います。実際私も「なんだそりゃ」と思わないでもありません。
ユークリッド空間の中だけで考えると、無限遠点を理解するのは難しいです。そのような点は(ユークリッド空間には)存在しないと言わざるを得ません。
なので、分かりやすそうな例を考えてみます。
奥行きのある絵や図を描く時の手法として、一点透視図法というものがあります。建物などを画面上のある特定の点(消失点)から伸びる直線に合わせて描くことで、遠近による歪みがある像をそれなりに正確に描くことができる手法です。
ここで、消失点から伸びる直線は、平面的に見ればもちろん平行ではありませんが、絵の中の世界では平行のはずの線です。ユークリッド空間では平行線はどこまで行っても交わりませんが、一点透視図法の空間では平行線は消失点で交わるのです。したがって、この消失点は、ユークリッド空間上の点に置き換えることができない点ということになります。
ここで、ユークリッド空間の概念を拡張して、無限遠点を導入します。すなわち、
- 平行線は交わらない
ではなく、
- 平行線は有限な点では交わらないが、無限遠点で交わる
ということにしてしまえば、一点透視図法からの変換も容易です。このような空間はもはやユークリッド空間とは言い難いですが。
逆に、一点透視図法の消失点は、絵の中の世界における無限遠点であると言えます。
無限遠点の概念は、他にも例えば3DCGの世界などで見ることができます。3Dオブジェクトをライティングする際に、平行光源という物を使い、例えば太陽光のような光を再現することがあります。現実における太陽はもちろん地球から約1auの距離にあって無限遠にある訳ではないので、厳密には太陽からの光は平行ではありませんが、平行としてしまってもおおむね問題なく描画できます(リアリティを求める場合はそれでも足りないかもしれませんが)。現実にはそのような光源は存在しませんが、もし存在すると仮定するなら、それは無限遠に位置する光源ということになります。
さて、無限遠点がなんとなく飲み込めて来たでしょうか。まだ飲み込めてなかったらすみません、もっといい説明の方法がありそうなら教えて下さい。ここから先は無限遠点の概念が分かってきたという体で話します。
楕円曲線上の加法群における無限遠点は、「 ![]() 軸に平行な直線と楕円曲線が交わる点のうち、有限な座標を持たないもの」と考えることができます。もちろん実際は交わりませんが、一点透視図法のように、グラフを傾ければ無限に伸ばした先で直線と楕円曲線が交わる消失点があるはずです。厳密とは言い難いですが、これが
軸に平行な直線と楕円曲線が交わる点のうち、有限な座標を持たないもの」と考えることができます。もちろん実際は交わりませんが、一点透視図法のように、グラフを傾ければ無限に伸ばした先で直線と楕円曲線が交わる消失点があるはずです。厳密とは言い難いですが、これが ![]() の正体です。
の正体です。
さらにこのまま考えを進めて、 ![]() と楕円曲線上の任意の点
と楕円曲線上の任意の点 ![]() を結ぶことを考えてみます。
を結ぶことを考えてみます。
![]() はもちろん仮想的な点であり、具体的な座標は分かりませんが、これを「消失点と任意の点を結ぶ」と同じように考えてみることができます。消失点から出た直線は一点透視図法の世界では互いに平行な直線です。同様に、無限遠点を通る直線も互いに平行とみなすと、
はもちろん仮想的な点であり、具体的な座標は分かりませんが、これを「消失点と任意の点を結ぶ」と同じように考えてみることができます。消失点から出た直線は一点透視図法の世界では互いに平行な直線です。同様に、無限遠点を通る直線も互いに平行とみなすと、 ![]() 軸に平行な直線が無限遠点を通るわけですから、「無限遠点を通る任意の直線は
軸に平行な直線が無限遠点を通るわけですから、「無限遠点を通る任意の直線は ![]() 軸と平行」と考えられます。
軸と平行」と考えられます。
![]() 軸に平行で点
軸に平行で点 ![]() を通る直線は、ユークリッド空間に戻ってくると、一意な一本の直線になり、その
を通る直線は、ユークリッド空間に戻ってくると、一意な一本の直線になり、その ![]() 座標は点
座標は点 ![]() の
の ![]() 座標ということになります。
座標ということになります。
先程のこの図で言うと、 ![]() と
と ![]() を結ぶ直線は無限遠点と
を結ぶ直線は無限遠点と ![]() を結ぶ直線であると言う事もできるわけです。
を結ぶ直線であると言う事もできるわけです。
さて、ここで ![]() について考えてみると、
について考えてみると、 ![]() と
と ![]() を通る直線と楕円曲線が作るもう一つの交点は
を通る直線と楕円曲線が作るもう一つの交点は ![]() となります。そして
となります。そして ![]() の
の ![]() 座標を反転した点は
座標を反転した点は ![]() 自身になるわけですから、
自身になるわけですから、 ![]() が成り立つ訳です。
が成り立つ訳です。
と言うのが、無限遠点 ![]() が楕円曲線上の加法群において「任意の点
が楕円曲線上の加法群において「任意の点 ![]() に関して、
に関して、 ![]() 」という演算が成り立つ(言い換えれば、
」という演算が成り立つ(言い換えれば、 ![]() は楕円曲線上の加法群における単位元である)ロジックかなと思います。だいぶ厳密性を欠いている気はしますが。
は楕円曲線上の加法群における単位元である)ロジックかなと思います。だいぶ厳密性を欠いている気はしますが。
無限遠点 ![]() について、ガッテンしていただけましたでしょうか。
について、ガッテンしていただけましたでしょうか。
加法の一般式
この節は数式がものすごく多くなってしまいどうしたものかと思わないでもないですが、この記事の目的の半分は自分がアルゴリズムを理解することなのでその道筋として書いておきます。同じようなことは色んな場所に書いてあって、Wikipediaの楕円曲線暗号の記事などを見てもいいと思います。ただ、筆者は見ただけではどうしてその計算になるのか分からなかったので細かく計算をやり直しています。
![]() 以外の点
以外の点 ![]() に関して、
に関して、 ![]() とすると、その座標を求めるには、
とすると、その座標を求めるには、![]() を通る直線の式
を通る直線の式 ![]() と楕円曲線の式
と楕円曲線の式 ![]() からなる連立方程式のを解くことになります。
からなる連立方程式のを解くことになります。
![]() とおくと、直線の式は
とおくと、直線の式は
![]()
![]() より、
より、 ![]() とおくと、
とおくと、 ![]() となります。
となります。
![]() を整理して、
を整理して、 ![]()
この3次式の根は ![]() なので、根と係数の関係より、
なので、根と係数の関係より、 ![]()
したがって、
![]()
![]()
が導けます。
2倍算
![]() のとき、すなわち
のとき、すなわち ![]() を計算する時は、上記の方法と同じように
を計算する時は、上記の方法と同じように ![]() を求めることはできず、
を求めることはできず、 ![]() における楕円曲線の接線を使います、つまり、
における楕円曲線の接線を使います、つまり、 ![]() の両辺を
の両辺を ![]() で微分して、
で微分して、
![]()
![]()
これに ![]() を代入したものが傾きとなるため、
を代入したものが傾きとなるため、
![]()
![]()
となります、ここまで来れば後は ![]() が異なる点である時と同じように求めることができます。
が異なる点である時と同じように求めることができます。
整数倍
これらの式から、整数倍を導くことができます。これはそれほど難しい話ではありません。楕円曲線上の任意の点について、 ![]() と繰り返せば整数倍です。
と繰り返せば整数倍です。
コンピューターで計算する際は愚直に繰り返すのではなく高速化を行うらしいのですが、そこは本題には関係ないので割愛します(実際の所、筆者がまだ理解してません)
楕円曲線「暗号」の話
この文書の主題は暗号です。ここまで楕円曲線上の加法群の話をして来ましたが、数学的な厳密性はさておき、これは暗号の話をする前置きです。
今までは実数座標系の楕円曲線について考えてきましたが、コンピューターでは実数は扱えないので、今後は有限体 ![]() 上の楕円曲線という物を扱います。
上の楕円曲線という物を扱います。
さて、今度は有限体 ![]() という概念が登場した訳ですので、少しばかりこれにも触れる必要があります。とは言え、ここらへんの話を始めると長くなる上に本筋から外れすぎるのでゆるふわな説明で留めたいところです。体より広範な概念である群についてもあまり説明せずに登場させてしまったことだし。
という概念が登場した訳ですので、少しばかりこれにも触れる必要があります。とは言え、ここらへんの話を始めると長くなる上に本筋から外れすぎるのでゆるふわな説明で留めたいところです。体より広範な概念である群についてもあまり説明せずに登場させてしまったことだし。
有限体は、四則演算が成立する有限個の元からなる集合です。プログラマーにとってわかりやすいのは整数型でしょうか。整数型の値はそのビット数で表すことのできる範囲しかとれないため、有限集合であり、四則演算が成り立つので有限体と言えます。
つまり、コンピューターで扱うのは有限体が限界であり、そのため、有限体 ![]() 上の楕円曲線という物に落とし込まないといけないのです。ここで、
上の楕円曲線という物に落とし込まないといけないのです。ここで、 ![]() は有限体を表す慣例的な記号であり、
は有限体を表す慣例的な記号であり、 ![]() は任意の素数です。
は任意の素数です。
上述のようにワイエルシュトラス型楕円曲線の式は ![]() で表されますが、これに相当する有限体
で表されますが、これに相当する有限体 ![]() 上の楕円曲線はこうです。
上の楕円曲線はこうです。
![]()
実際に暗号化に使う ![]() はとても大きな数を使いますが、例によって簡単にするために
はとても大きな数を使いますが、例によって簡単にするために ![]() で考えてみます。
で考えてみます。
楕円曲線は上で使った例から ![]() の曲線を持ってきてみましょう。つまり、
の曲線を持ってきてみましょう。つまり、
![]()
というものについて考えます。
有限体 ![]() の元は
の元は ![]() の5つです。
の5つです。
![]() の時、
の時、 ![]() で、これを満たすのは
で、これを満たすのは ![]() です。
です。
![]() の時、
の時、 ![]() で、これを満たす
で、これを満たす ![]() はありません。
はありません。
![]() の時、
の時、 ![]() で、これを満たすのは
で、これを満たすのは ![]() です。
です。
![]() の時、
の時、 ![]() で、これを満たすのは
で、これを満たすのは ![]() です。
です。
![]() の時、
の時、 ![]() で、これを満たすのは
で、これを満たすのは ![]() です。
です。
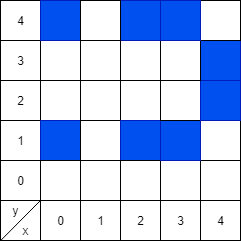
という訳で、 ![]() 上の楕円曲線
上の楕円曲線 ![]() はこうなります。
はこうなります。
うーむ、もはや楕円でもなければ曲線でもない。
さて、このような点に関して、先程の2倍算や整数倍を実行するとどうなるか。
例えば ![]() とすると、
とすると、
![]()
![]()
より、
![]()
となります。ただ、これだと有限体 ![]() 上の点ではないので、変換を挟む必要があります。
上の点ではないので、変換を挟む必要があります。
すなわち、 ![]() を
を ![]() で
で ![]() 倍したときに
倍したときに ![]() になる数とみなすと、これは
になる数とみなすと、これは ![]() が対応します。
が対応します。
同様に、 ![]() は、
は、 ![]() 倍して
倍して ![]() となる数とみなすと、これは
となる数とみなすと、これは ![]() であることが分かります。したがって、
であることが分かります。したがって、
![]()
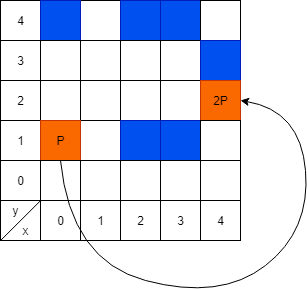
これを図示すると、このようになります。
このように、有限体 ![]() 上の楕円曲線でも加法や整数倍が成り立ち、
上の楕円曲線でも加法や整数倍が成り立ち、 ![]() 以外の点同士の加算は必ず他の楕円曲線上の点もしくは
以外の点同士の加算は必ず他の楕円曲線上の点もしくは ![]() になります。
になります。
点の個数は有限なので、 ![]() と順に求めるといずれ
と順に求めるといずれ ![]() に至り、また
に至り、また![]() に戻ってくる巡回群となります。
に戻ってくる巡回群となります。
ここで、 点 ![]() を起点とし位数
を起点とし位数 ![]() の巡回群内の任意の点
の巡回群内の任意の点 ![]() について、
について、 ![]() となるような整数
となるような整数 ![]() が一意に定まることが分かります。
が一意に定まることが分かります。
このような整数 ![]() を求めるのは離散対数問題なので、解読は容易ではありません。つまり、
を求めるのは離散対数問題なので、解読は容易ではありません。つまり、 ![]() を総当りで求めるくらいの方法しかないので、
を総当りで求めるくらいの方法しかないので、 ![]() が十分に大きければ現実的な時間で解くことができない問題となります。つまり、
が十分に大きければ現実的な時間で解くことができない問題となります。つまり、 ![]() を公開鍵とすると、
を公開鍵とすると、 ![]() が秘密鍵ということになります。
が秘密鍵ということになります。
![]() が十分に大きくなるためには
が十分に大きくなるためには ![]() が十分大きくなければならないので、実際の楕円曲線暗号ではそうなるように楕円曲線の種類や巡回群の起点
が十分大きくなければならないので、実際の楕円曲線暗号ではそうなるように楕円曲線の種類や巡回群の起点 ![]() が選ばれています。少なくとも、例示したような形の楕円曲線では一瞬で破られてしまいます。
が選ばれています。少なくとも、例示したような形の楕円曲線では一瞬で破られてしまいます。
終わりに
当初の予定では、この後前回と同じようにごく簡単な例で暗号化と復号までやってみようと思っていたのですが、思った以上に理論と計算で手間取ってしまい時間がなくなったので、一旦ここで終了としたいと思います。私自身の知識も、「曲線をどうやって暗号に使ってるんだろうなー」みたいな所からそれなりに先に進めたので良しとしたい所です。
それではまた。
おたより発掘
エンジニアブログに楕円曲線が詳しくのってて楕円曲線好きとして嬉しい...!(そこ)https://t.co/mEurAeJMe9
— しらたき (@srtk86) August 17, 2019