🔗 ChatGPTのしくみとAI理論の根源に迫る:(5/16)古典の「ニューラルネット」をおさらいする(翻訳)
では、前章で説明した画像認識のようなタスクで使われる典型的なモデルは、実際にはどんなふうに振る舞うのでしょうか?
本記事執筆時点で、画像認識方面で最もよく知られていて、かつ成功を収めているモデルは、 ニューラルネットを使う方法です。ニューラルネットは、人間の脳がどのように働くかをシンプルな形で理想化したものとみなすことが可能であり、早くも1940年代には現在のものとかなり近い形のものが発明されています。
人間の脳には約1000億個のニューロン(神経細胞)があり、それぞれが1秒間に最大1000回もの電気パルスを発生させることが可能です。ニューロンは複雑な網の目のように互いに入り組んでつながっており、各ニューロンは木のように多数の枝に分かれ、おそらく何千もの他のニューロンに電気信号を送信できます。
そして、ある瞬間にどのニューロンが電気パルスを発生させるかは、大まかには他のニューロンからどのような種類のパルスを受け取ったかで決定されます。つまり、ニューロンのさまざまな接続ごとに、異なる「重み(weight)」パラメータが関与する形になっています。
私たちが「映像を見る」とき、その映像の光(光子)が目の奥にある「視細胞(photoreceptor)」に達すると、神経細胞でパルス状の電気信号が発生します。この神経細胞は他のさまざまな神経細胞と網の目のようにつながっており、最終的に電気信号は神経細胞の層全体を駆け抜けます。
そして、私たちはこの過程を経ることで画像を「認識」し、最終的には「"2"が見える」という「思考」を形成します。最終的には「2」という単語を声に出して言ったりもするでしょう。
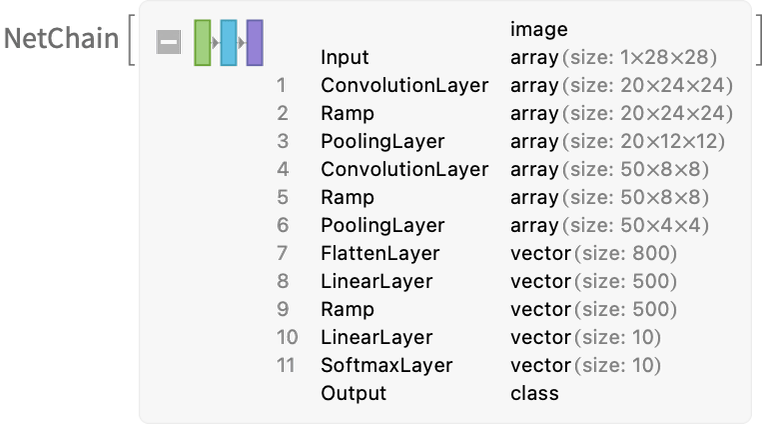
前章で説明した「ブラックボックス関数」は、今述べたようなニューラルネットを「数学化した(mathematicized)」ものです。このブラックボックス関数には、以下のように(たまたま)11の層が存在しています(ただしコアとなる層は4つだけです)。
原注
ご注意いただきたいのですが、上のブラックボックス関数は、このニューラルネットから「理論的な根拠に基づいて導き出したもの」ではありません。1998年にエンジニアリングの一環として構築したブラックボックス関数が、たまたま使い物になることがわかった、というだけの代物です。
(もちろん、このブラックボックス関数は、私たちの脳が生物学的な進化の過程で生み出したニューラルネットの振る舞いと大差ありません)
さて、このニューラルネットとやらは、どうやって「モノを認識」するのでしょうか?ここを理解するうえで重要な鍵となるのは、「アトラクター(attractor)」という概念です。
アトラクターを理解するために、以下のような1と2の手書きの画像で考えてみましょう(訳注: この時点では1や2の画像の配置に意味はありません)。
上の図にある"1"らしき画像たちを、どうにかして図の中のある場所に引き寄せ、"2"らしき画像たちを図の中にある別の場所に引き寄せたいとしましょう。
言い換えれば、ある画像が「"2"というよりは"1"に近い」と思われる場合、その「近さ」に応じて、その画像を"1"の集団に近い位置に移動し、逆に「"1"というよりは"2"に近い」についても同様に、その画像を近さに応じて"2"の集団に近い位置に移動したい、ということです。
もう少し分かりやすい例えに言い換えてみましょう。
ある平面上で、さまざまな特定の位置を、平面上の点の配置で示しているとします。これは、地図上にいくつものコンビニが赤い点で表示されていると考えるとよいでしょう。
このとき、自分が地図上のどこにいても、確実に最寄りのコンビニに行きたい(つまり、最寄りのコンビニがあるのに、それより遠いコンビニに間違って行きたくない)とします。
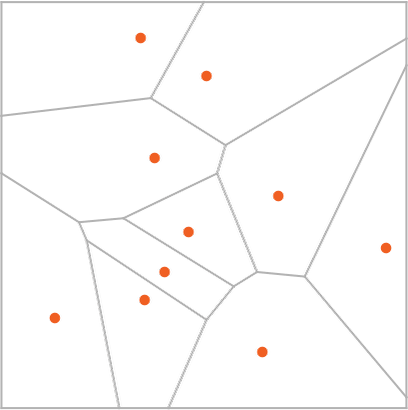
このような振る舞いは、その平面(地図)を、一種の理想化された「分水嶺(watershed)」で区切られたいくつもの領域である「アトラクター盆地(attractor basin)」に分割することで、うまい具合に抽象化して表現できます。
訳注
上の図を山岳地帯の地図に見立てたとすると、灰色の線は尾根、灰色の線で囲まれている領域は盆地、そして赤い点は盆地の中で最も標高の低い場所、と考えるとよいでしょう。
参考までに、等高線を加えた手書きの図を添えます。赤い点は盆地の「最も低い点」であることにご注意ください。
このように見立てたうえで、アトラクター盆地に球を置くと、必ず最寄りの赤い点まで転がることになります。そして、決して最寄りでない赤い点に球が転がり寄っていくことはありません。
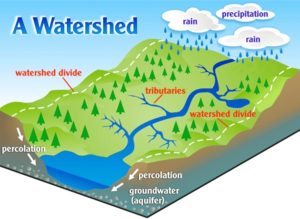
参考までに、分水嶺(watershed)を表す模式図も以下に引用します。水は、分水嶺を超えて流れることはありません。
What is a Watershed? - Riverside-Corona Resource Conservation Districtより
「ある画像がどの数字に最も似ているかを認識する作業」は、このように「自分から見てどの赤い点が最も近いかを直接的に確認できる」認識タスクに置き換えて考えることも可能なのです。
原注
上で紹介した「ボロノイ図(Voronoi diagram)」は、本来は2次元のユークリッド空間で点と点を分離するためのものですが、数字の画像認識という課題は、これとよく似た操作を、各画像の全ピクセルの灰色の濃さ(グレーレベル)情報を集めた784次元空間で行っていると見なすことが可能です1。
さて、ニューラルネットに「画像認識タスク」を実行させるとしたら、どうしたらよいでしょうか?
最初は、画像と関係のない、うんとシンプルなケースから考えてみましょう。
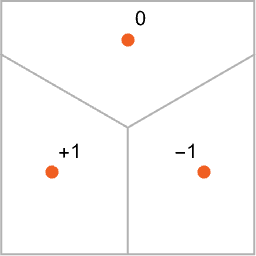
ここでの目標は、図の中での位置を表す ![]() という座標2に対応する入力を受け取ったときに、その入力から見て、
という座標2に対応する入力を受け取ったときに、その入力から見て、0、-1、+1の3つの点のどれか最も近い点なのかを判断させることです。
言い換えると、「1.0〜-1.0の範囲でたとえば![]() という具合に入力を与えると、
という具合に入力を与えると、0、-1、+1のどれかを返す」、そんな![]() 関数をニューラルネットで以下のように計算させたいのです。
関数をニューラルネットで以下のように計算させたいのです。
では、そのような計算をニューラルネットで実現するにはどうすればよいのでしょうか。
最終的にニューラルネットは、理想化された「ニューロン(neuron)」を連結した集合体で、通常は、上から下に縦方向に進む層の重なりという形で表現されます。
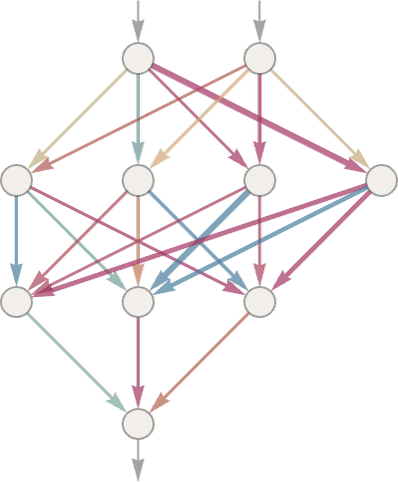
以下は簡単なニューラルネットのサンプルです。
個別の「ニューロン」(上図の円)は、単純な数値関数3を評価するようにセットアップされています。
このニューラルネットを実際に「使う」には、ニューラルネットの一番上から、![]() や
や![]() という座標などの形で数値情報を入力し、各層のニューロンに「関数を評価」させ、その結果をネットワークを通して下に送り、最終的に一番下から最終結果を取り出せばよいのです。
という座標などの形で数値情報を入力し、各層のニューロンに「関数を評価」させ、その結果をネットワークを通して下に送り、最終的に一番下から最終結果を取り出せばよいのです。
生物学を元にした伝統的なセットアップでは、個別のニューロンは実質的に、上の層のニューロンからつながる特定の「入力接続(incoming connection)」をいくつも持っており、それぞれの接続には特定の「重み(weight)」というパラメータが、さまざまな正の数や負の数として割り当てられています4。
あるニューロンの値は、「その上のニューロン」たちからやってくるさまざまな出力値に、その値がやってくる接続ごとに設定されている重みを掛け、それらを合計した値に、さらに何らかの定数を足し、最後に「しきい値関数(thresholding function)」(活性化関数(activation function))を適用することで、決定されます。
原注
数学的には、あるニューロンに![]() という入力が与えられたときに、何らかの活性化関数
という入力が与えられたときに、何らかの活性化関数![]() を計算するのと同じです5。ただし、一般に重み
を計算するのと同じです5。ただし、一般に重み![]() と定数
と定数![]() はネットワーク内のニューロンごとに異なる値を選択しますが、この活性化関数
はネットワーク内のニューロンごとに異なる値を選択しますが、この活性化関数![]() の形は、どのニューロンでも同じになるのが普通です。
の形は、どのニューロンでも同じになるのが普通です。
![]() の計算自体は、行列の乗算と行列の加算という単純な(ただし大量の)線形代数の計算問題に過ぎません。
の計算自体は、行列の乗算と行列の加算という単純な(ただし大量の)線形代数の計算問題に過ぎません。
しかしそれを囲んでいる活性化関数![]() は、ここに非線形性(nonlinearity)を導入するという重要な役割を果たしています6。そして非線形の活性化関数を導入することで、線形性では決して得られない、自明でない振る舞い(nontrivial behavior)を得られるのです。
は、ここに非線形性(nonlinearity)を導入するという重要な役割を果たしています6。そして非線形の活性化関数を導入することで、線形性では決して得られない、自明でない振る舞い(nontrivial behavior)を得られるのです。
活性化関数にはさまざまなものが使われますが、ここではRamp(ReLU)を使うことにしましょう(下図の一番左)。
ニューラルネットにどんなタスクを実行させたいかに応じて(あるいは同じことですが、どんな機能全体を評価させたいかに応じて)、選ぶべき重み付けの値は異なってきます。
原注
この後の章で後述しますが、これらの重みは通常、欲しい出力のさまざまなサンプルを与えて、機械学習の形でニューラルネットを「トレーニング(training: 訓練)」することで決定されます。
ニューラルネットでどんな重み付けを選ぼうと、最終的には何らかの全体的な数学的関数に対応付けられることになります。そうした数学的関数をここに書き出したところで煩雑になるだけですが、たとえば上の例に対応する関数なら以下のような感じになるでしょう。
皆さんの知りたいChatGPTのニューラルネットも、こんな感じの数学的関数に対応付けられるという点では同じなのですが、その関数の項(term)の個数は実質的に数十億個レベルになるでしょう。
それはともかく、個別のニューロンの話に戻りましょう。
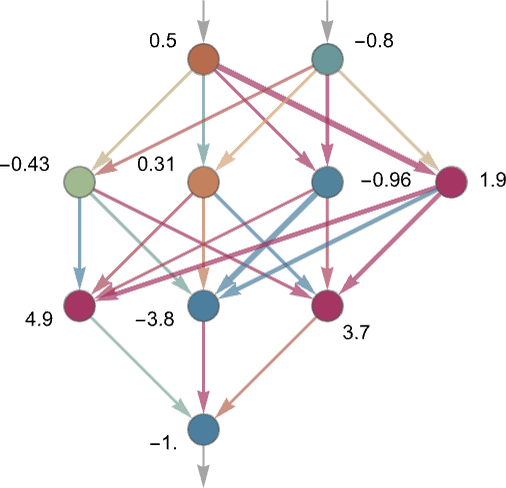
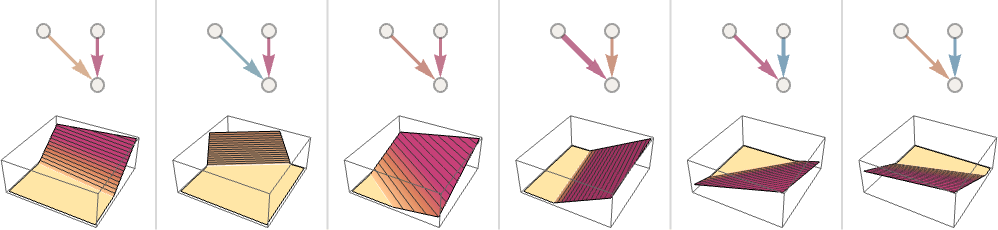
以下では「2つの入力(![]() と
と![]() )を持つ1つのニューロン」が、そこに設定される重みや定数(および、活性化関数としての
)を持つ1つのニューロン」が、そこに設定される重みや定数(および、活性化関数としてのRamp関数)をさまざまに変えることで計算結果がどのように変わるかという例をいくつか示しています。
薄い青矢印: 正の重み(値: 小)
濃い青矢印: 正の重み(値: 大)
薄い赤矢印: 負の重み(値: 小)
濃い赤矢印: 負の重み(値: 大)
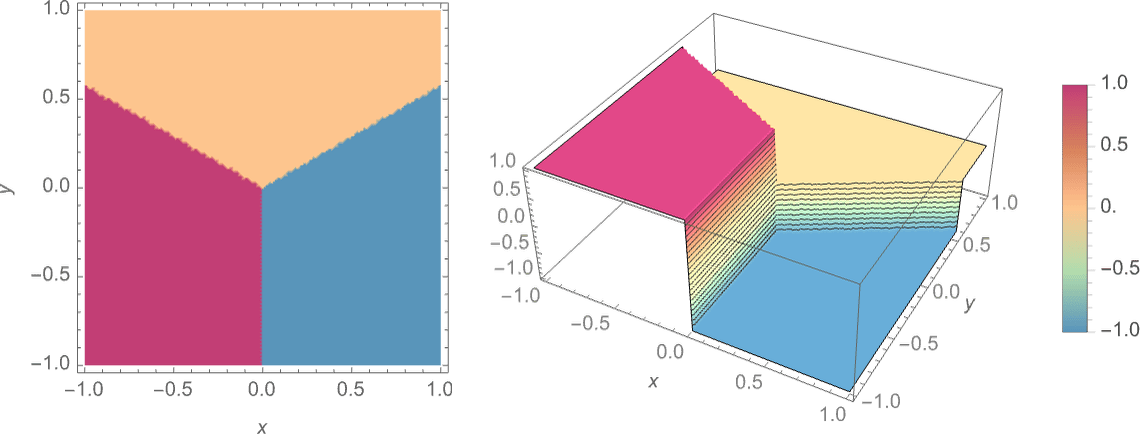
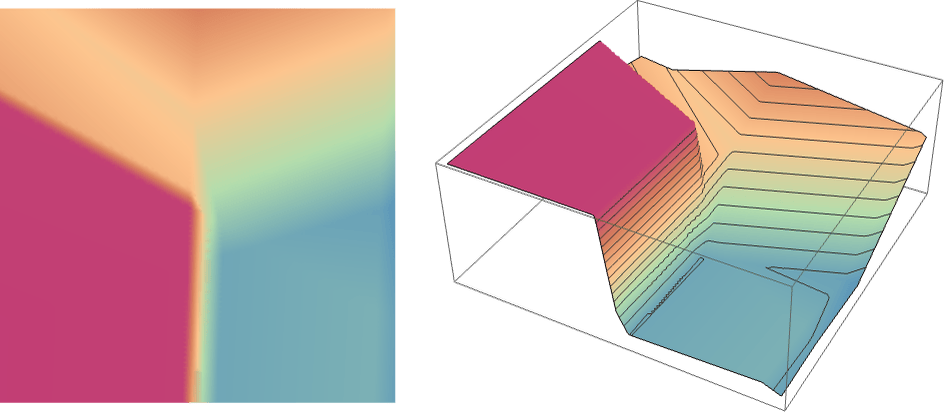
しかし上のようなたった3つのニューロンでできたニューラルネットワークではなく、もっとずっと大規模なニューラルネットワークでは、以下のような計算結果になります。
この計算結果は、上で示した理想的な「最近接点(nearest point)」関数のようにくっきり3色に分かれたものではありませんが、それに迫る結果になっています。
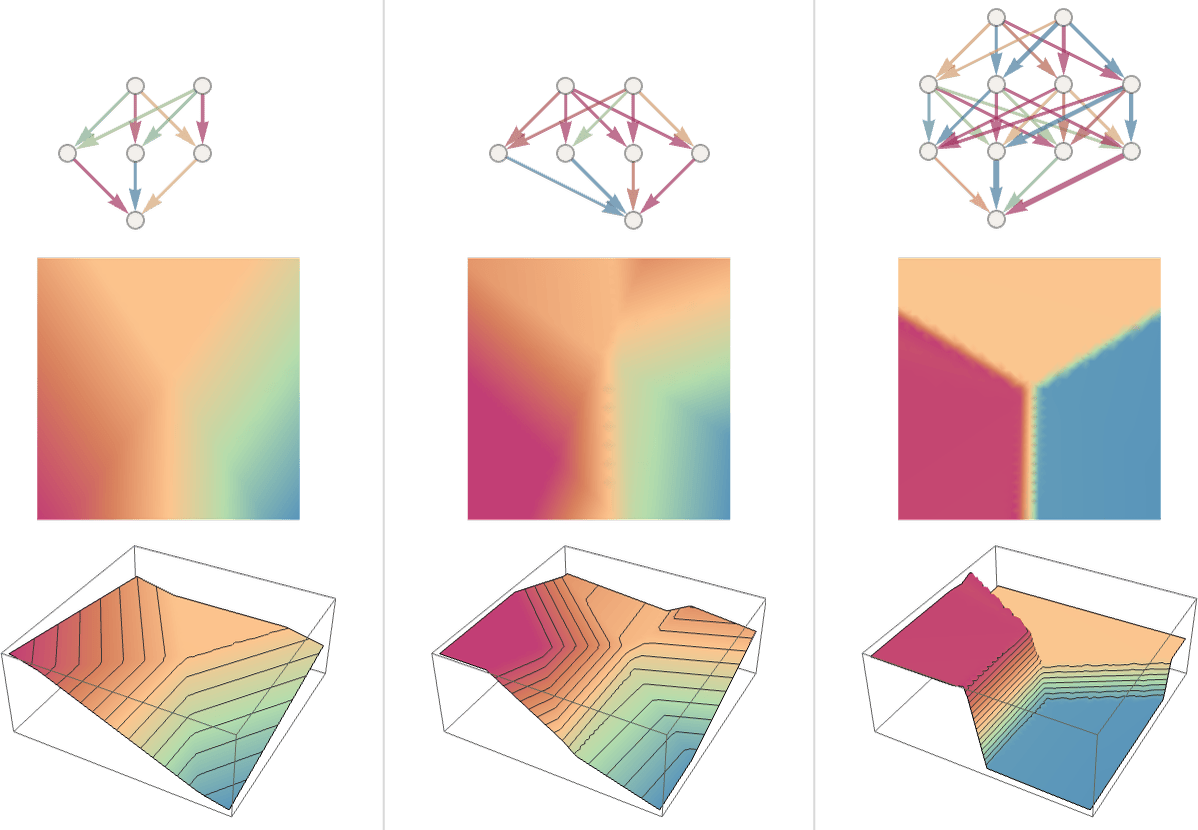
次は、他のニューラルネットではどうなるのか見てみましょう。
以下の3つのケースは、後で説明するように、どれも事前に機械学習を使って最適な重みを選ばせてあります。そして、その重みを持つニューラルネットの計算結果を、その下に縦に並んでいる2つの3色グラフ(上から見た図と鳥瞰図)で示してあります。
一般に、ネットワークの規模が大きくなればなるほど、くっきりと3色に分かれた理想的なグラフに近くなることがわかっています。また一般に、どんなアトラクター盆地であろうと、球を盆地の「どこか」に置きさえすれば、欲しい答えの場所(盆地の一番低いところにある赤い点)まで球は自動的に転がってくれる、つまり欲しい答え(=一番近い赤い点はどこか)を得られます。
しかしニューラルネットといえども、球が境界線上(色と色の境目となる尾根のような部分)に置かれると、球がどっち側のアトラクター盆地に転がっていくかを決めにくいため、面倒が増える可能性があります。
今ここで話しているような「0か1か-1か」といったシンプルな数学的スタイルの「認識タスク」であれば、どれが正しい答えかぐらいは誰が見てもわかるので、何の問題もありません。
しかし手書きの数字を認識するという問題は、おいそれと簡単には解けません。"2"と書いたつもりの字が汚すぎて"7"に見えてしまう場合は、どうジャッジすればいいか?といった問題がいろいろ生じてしまいます。
それでも、ニューラルネットが手書き数字をいかにして見分けるか、という問いかけは有効なのです。
以下の処理済みの図に、その方法の一端を垣間見ることができます。
図形がどの数字を表しているかを、純粋に「数学的な手法」だけで区別できるかと聞かれたら、無理と答えるしかありません。図形を見分けているのはあくまで「ニューラルネット」であり、数学ではないのです。ニューラルネットは数学などとは無関係に、ひたすら「ニューラルネットができること」をやっているに過ぎません。
しかしそれでもニューラルネットは、人間が普段当たり前にやっているのと同じように、かなりよい感じで図形がどの数字であるかを区別できているようです。
今度は、数字の区別よりもっと複雑な問題を見ていきましょう。
たとえば、イヌやネコの写真がたくさんあるとします。そして都合のいいことに、イヌやネコを区別する訓練を受けたニューラルネットも使える状況にあるとします。
このニューラルネットに、イヌやネコの写真を区別する「お仕事」をさせたとすると、おそらく以下のサンプル画像のような感じでイヌやネコの写真が平面上に分類・配置されるでしょう。
しかしイヌネコ区別問題ともなると、「そもそも正しい答えとは何なのか」という判断基準すら怪しくなってきます。「イヌにネコのコスプレをさせたら、それはイヌと判定すべきか?」など、言い出したらキリがありません。
ニューラルネットにどんな入力画像を与えたとしても、ニューラルネットは、あくまで「人間と同じように」判定を下すだけであることにご注意ください。ニューラルネットが出力する答えが「正しいか間違っているか」を問題にしているのではなく、ニューラルネットが下す判断が人間と同じかどうかを問題にしているのです。
ニューラルネットがこのように人間に近い形で振る舞う理由は、「根本となる第一原理から論理的に導き出す」形では説明できておらず、経験的にそう振る舞うこと以外、何もわかっていません。
しかし、だからこそニューラルネットは有用であり、人間らしい振る舞いを何らかの形でキャプチャできているのです。
あなたがネコ写真を見せられて「これがネコだと思う理由を説明してよ」と質問されれば「そりゃまぁ、耳が猫耳らしくとんがってるし」などと苦し紛れにいくつか説明を並べるぐらいはできるでしょう。
しかし、その画像がネコの写真であると判定する適切な方法を客観的な言葉で完全に説明しつくそうとすると、途端に困ってしまいます。せいぜい「ぼくの脳みそが"これはネコだ"って言ってるから、ネコだとしか言いようがないんだけどなぁ...」どまりでしょう。
しかし人間の頭をかち割って、人間の脳がネコ写真をどうやってネコだと認識するかを「徹底的に調べる」方法は、(少なくとも今のところは)ありません。
では、(本物の人間の脳ではなく)人工的なニューラルネットなら、かち割って中を徹底的に調べることは可能でしょうか?
さすがに人工的なニューラルネットなら、ネコ写真を見せられたときに個別の「ニューロン」がどう反応するか、ぐらいは普通に調べられます。しかし一般には、ニューラルネットがどのようにして判定を下すかという基本的な処理方法すら満足にわかっていません。
上述の「最近接点」問題で取り上げた最後のニューラルネット(横並びの3つの図の一番右)では、17個のニューロンを使いました。先ほどの手書き数字認識用のニューラルネットでは、2190個のニューロンを使いました。そして、イヌネコ画像を判定するためのニューラルネットでは、60,650個のニューロンを使いました。
一般的な処理を扱う場合、この60,650次元の空間をビジュアル表示しようとすると、それだけでかなり大変な作業になるでしょう。
しかし幸いなことに、このニューラルネットは画像認識専用に特化しています。
ニューラルネットでは多数のニューロン層が使われていますが、画像認識専用のニューラルネットであれば、その中からどのニューロン層を取り出しても、そのニューラルネットが認識しようとする画像のピクセル情報を、そのまま縦横に並べて表示した画像と同じ並びになるのが普通です。画像認識以外の処理では、こうはいきません。
以下の典型的なネコ画像を例に取るとしましょう。
上のネコ画像をニューラルネットで処理する場合、ニューラルネットの第1層を取り出してみると、以下のように元のネコ画像から派生したさまざまな画像の集まりとして表現できます。派生ネコ画像の大半は、人間が見ても「背景抜きのネコ画像」や「ネコの輪郭線」といった感じで十分解釈可能です。
これが以下のようにニューラルネットの第10層まで進むと、どんな処理を行っているかすら判然としなくなります。
しかし一般論としては、ニューラルネットがネコ画像の「何らかの特徴(feature)を取り出して」、それを元に何の画像であるかを認識している、と考えてもよさそうではあります。
そうやってニューラルネットが捉えた特徴の中には、猫耳かどうかという特徴もおそらく含まれているでしょうが、「これこそが猫耳である」と呼んでも差し支えなさそうな、わかりやすい画像的特徴として手に入れられるかというと、ほとんどの場合無理でしょう。
私たちの脳の中でも、ニューラルネットの場合と同じような感じで特徴を捉えていることがわかればよいのですが、残念ながら、ほぼ何もわかっていません。
しかし、今回取り上げたニューラルネットの最初の数層で捉えた画像の特徴のさまざまな側面(物体の輪郭など)が、脳の視覚処理の第1層で捉えられる特徴のそれに近いと思われる点は、注目に値します。
しかし、たとえばニューラルネットが「ネコを認識するしくみ」を理論化して、理論で完全に説明しつくすのは、並大抵ではありません。
「やった、このニューラルネットはネコを認識できるぞ!」ということをめでたく突き止めたとして、「それがどの程度困難な問題なのか(ニューロンや層をどれだけ必要とするか)」については割とすぐ見当をつけられます。
しかし少なくとも、そのニューラルネットの振る舞いを「これこれこういう理由で、ニューラルネットはネコをずばり認識できるのです」というふうに何もかも理詰めで説明しつくす方法は、残念ながら存在しません。
原注
おそらく、ニューラルネットが行っている計算処理は、真の意味で「還元不可能(irreducible)」なのでしょう。すなわち、ニューラルネットの処理はこれ以上シンプルな計算に置き換えようがなく、ニューラルネットとしてのステップを明示的にたどる以外に、処理のステップを追いかける方法が存在しないということです。
さもなければ、私たちがニューラルネットの科学をまだ本当の意味で解明できておらず、そこで起こっている処理を要約するため「自然法則」を発見していないだけなのかもしれません。
そして私たちはChatGPTでも、ニューラルネットで私たちが遭遇したのと同じような「理詰めで説明できない」問題に直面することになるのです。ChatGPT内部で起きていることを言葉で説明しつくす方法が果たして存在するのかどうか、それすらまだ明らかになっていません。
しかし、ChatGPTの主戦場である「言語という世界」には、汲んでも尽きぬほどに豊かな実りと、私たち人間が言語について蓄積してきた莫大な経験値が満ち溢れています。私たちはもしかすると、画像という世界を主戦場とするよりも、この言語という世界でこそ豊かな成果を得られる可能性だってあるのです。
次回: (6/16)機械学習とニューラルネットのトレーニング
関連記事
- 訳注: ここで言う「次元」は、単なるパラメータの個数であると考えても構いません。 ↩
-
訳注: このようにベクトルを一般的な
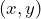 ではなく
ではなく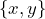 で表記するのは、著者Stephen Wolframが開発したMathematicaという数式処理ソフトウェアで使われている記法が由来です。 ↩
で表記するのは、著者Stephen Wolframが開発したMathematicaという数式処理ソフトウェアで使われている記法が由来です。 ↩
- 訳注: この数値関数は、数値を受け取って数値を出力する、単なる説明のためのものであり、画像認識そのものとは無関係です。 ↩
- 訳注: 図でニューロンごとに表示されている数値は、接続ごとの重みではなく、そのニューロンの出力の数値を表しています。図には、重みの数値は書かれていないことにご注意ください。 ↩
-
訳注: 関数を数学で一般的な
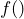 ではなく
ではなく![Rendered by QuickLaTeX.com f[]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-39c2761a1f872aabeb3fc5edef709db0_l3.png) で表記するのも、Mathematica流です。 ↩
で表記するのも、Mathematica流です。 ↩
-
訳注: 内側の
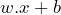 は線形代数の演算であり当然線形ですが、それを囲む活性化関数
は線形代数の演算であり当然線形ですが、それを囲む活性化関数![Rendered by QuickLaTeX.com f[]](https://techracho.bpsinc.jp/wp-content/ql-cache/quicklatex.com-39c2761a1f872aabeb3fc5edef709db0_l3.png) が非線形であることが重要です。1960年代末のニューラルネットワーク研究の初期に、XOR演算は線形分離不可能なため、XOR演算は線形なパーセプトロンでは学習不可能であることがミンスキーらによって指摘され、XORという基本的な論理演算が学習不可能という衝撃的な結果によって、一時はニューラルネットワーク研究の灯が消えそうになるほどでしたが、後に活性化関数を何らかの形で非線形にすれば克服可能であることが判明し、突破口となりました。すなわち活性化関数はぜひとも非線形でなければならないのです。ただしこのことは、XOR演算をニューラルネットワークで組めないという意味ではありません。電気回路でXORロジックを実現可能であるのと同様にパーセプトロンでもXORロジックを組むこと自体は可能ですが、パーセプトロンが線形である限り、XORロジックを学習で獲得することは本質的に不可能です。なぜXORロジックだけが線形分離不可能なのかは、自分で調べてみると面白いでしょう。参考: Linear Separability: OR vs XOR - YouTube ↩
が非線形であることが重要です。1960年代末のニューラルネットワーク研究の初期に、XOR演算は線形分離不可能なため、XOR演算は線形なパーセプトロンでは学習不可能であることがミンスキーらによって指摘され、XORという基本的な論理演算が学習不可能という衝撃的な結果によって、一時はニューラルネットワーク研究の灯が消えそうになるほどでしたが、後に活性化関数を何らかの形で非線形にすれば克服可能であることが判明し、突破口となりました。すなわち活性化関数はぜひとも非線形でなければならないのです。ただしこのことは、XOR演算をニューラルネットワークで組めないという意味ではありません。電気回路でXORロジックを実現可能であるのと同様にパーセプトロンでもXORロジックを組むこと自体は可能ですが、パーセプトロンが線形である限り、XORロジックを学習で獲得することは本質的に不可能です。なぜXORロジックだけが線形分離不可能なのかは、自分で調べてみると面白いでしょう。参考: Linear Separability: OR vs XOR - YouTube ↩

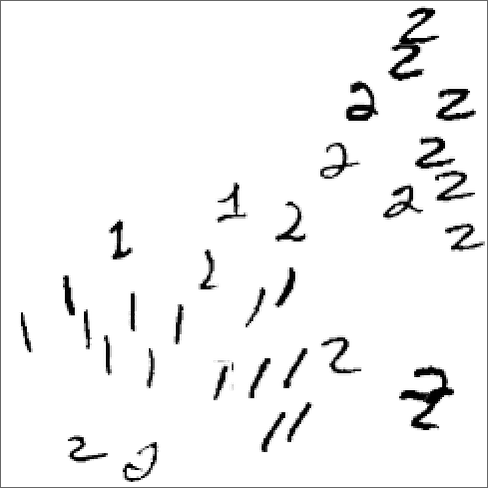


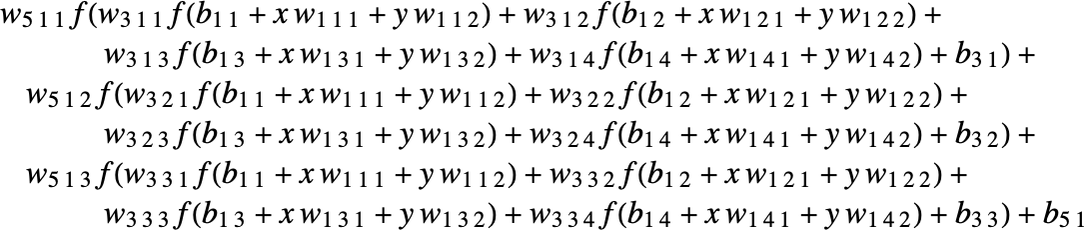





概要
原文サイトのCreative Commons BY-NC-SA 4.0を継承する形で翻訳・公開いたします。
日本語タイトルは内容に即したものにしました。原文が長大なので、章ごとに16分割して公開します。
スタイルについては、かっこ書きを注釈にする、図をblockquoteにするなどフォーマットを適宜改善し、文面に適宜強調も加えています。
元記事は、2023年2月の公開時点における、ChatGPTを題材とした生成AIの基本概念について解説したものです。実際の商用AIでは有害コンテンツのフィルタなどさまざまな制御も加えられているため、そうした商用の生成AIが確率をベースとしつつ、確率以外の制御も加わっていることを知っておいてください。
本記事の原文を開いて、そこに掲載されている図版をクリックすると、自分のコンピュータでもすぐに実行して試せるWolfram言語コードが自動的にクリップボードにコピーされるようになっています。
参考: ニューラルネットワーク - Wikipedia
コモンズ証 - 表示 - 非営利 - 継承 4.0 国際 - Creative Commons