🔗 ChatGPTのしくみとAI理論の根源に迫る:（4/16）人間らしいタスクをこなせるモデルとは（翻訳）
前章の例では、数世紀前から知られている単純な古典物理学に由来する、「単純な数学が通用する」 数値データのモデルを作ってみました。
しかし、ChatGPTの場合は、人間の脳が生成するような、人間の言葉を使ったテキストのモデルを作ってあげなければなりません。
ただし残念ながら、古典物理学のような「単純な数学」で楽に扱えるようなものは、AIについては見つかっていません（少なくとも今のところは）。
では、ChatGPTで使われるモデルとは、どのようなものなのでしょうか。
テキスト生成の話をする前に、これも同じぐらい人間らしいタスクである「画像認識（recognizing images）」を扱ってみましょう。
画像認識の簡単な例として、以下の数字を認識させることを考えてみます（はい、これは今や古典となった機械学習の典型的なサンプルでもあります）。
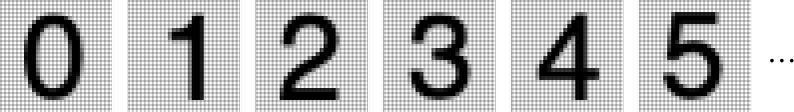
この手の画像認識でできそうなことのひとつといえば、とにかく以下のような数字のサンプル画像を大量にかき集めることです。
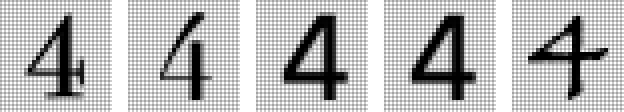
この場合、入力から受け取った画像が特定の数字に対応しているかどうかを調べたければ、手持ちのサンプル画像のどれかと何から何まで完全に一致するかどうかをピクセル単位で愚直に比較しまくればよい、という考え方も一応可能でしょう。
しかし人間の視覚は、手持ちのサンプルと完全一致するものだけを認識する、などという融通の効かない方法ではなく、もっと柔軟な方法を使っているものです。人間なら、たとえば以下のような手書きの数字や、ありとあらゆる方法でよじれて変形したサンプル画像の数字すら楽々と認識できます。
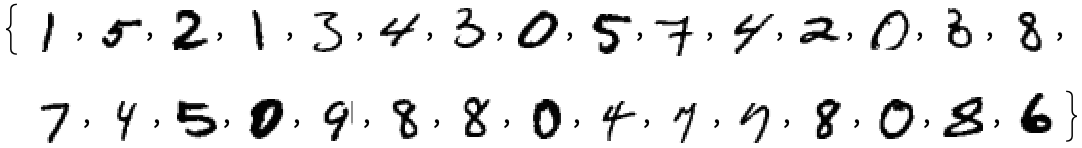
仮に、上の数字画像データを認識するためのモデルを首尾よく作ることに成功したとしましょう。そしてそのモデルを使って、「入力
を受け取り、特定の
と
について
を計算して云々」という一次関数並のシンプルさで計算できれば万々歳でしょう。
さて、ある数値を表している1つの画像は、たくさんのピクセル（pixel）が集まってできています。そのたくさんのピクセルの1つ1つの濃さを、仮に
で表したとしましょう。つまり、
は最初のピクセル、
は2番目のピクセル...という具合に、
までのたくさんのグレイスケールデータがあり、その中の1つをとするわけです。
このからまでの多数のピクセル値（=灰色の濃さ）を一度に渡されると、それらを評価して、元の画像が表す数字を見事導き出して「この画像の数値は7です」などと正しく答えてくれる、そんな都合の良い関数はこの世に存在するのでしょうか？
答えを言ってしまえば、そういう都合の良い関数は「存在します」。
原注
当然ながら、そのような関数は、のようなシンプルでわかりやすい形にはなってくれません（この種の関数では、数学的演算が50万回程度必要になるのが普通です）。
しかしそれでも、この関数に画像のピクセル値（灰色の濃さ）の集合を入力してやれば、画像が表している数値が出力されます（このような関数の構築方法や、ニューラルネットワークの考え方についてはこの後の別の章で解説します）。
しかし今は、この関数をブラックボックスとして扱いましょう。
たとえば、この関数に以下の手書き数字画像（ピクセル値の配列）を入力すると、それに対応する数値が出力されます。
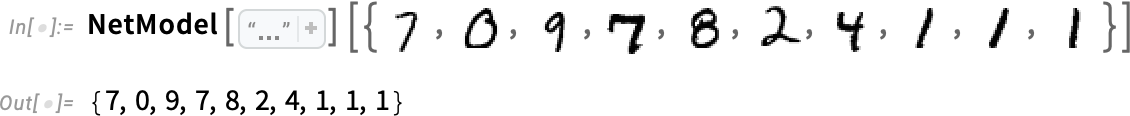
しかしこのやり方は、本当に現場でうまくいくのでしょうか？
たとえば以下のように、ある数値の画像を徐々にぼかして、どこまでぼかせるかを試してみたとしましょう（ここでは"2"を使います）。
この関数は、しばらくの間は引き続き数値を正しく「認識」できるでしょう。しかしある程度以上ぼかした画像になると「見失って」しまい、「誤った」結果を出力するようになります。
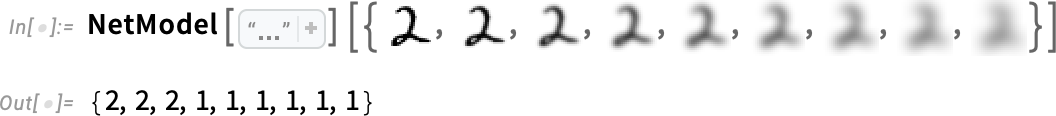
しかし、ぼかした画像から得た数値が「間違っている」とどうして言い切れるのでしょうか？この場合、"2"を表す画像を単純に少しずつぼかしたのですから、どんなにぼかしたとしても、"2"と認識するのが正しい、ここまでは確かです。
しかし、目的が「人間が画像を認識するときのモデル」を再現することであれば、「数値が合ってる」「数値が間違ってる」ということを問題にするのは筋違いと言えます。
ここでの適切な問いとは、「ぼかす前には何の画像だったかを知らないまま、そうしたぼかし画像を人間が見せられると、人間はどう反応するのか」です。
そして、その関数から得られる結果が、人間の認識方法と一般的に合致すれば、それは「良いモデル（good model）」であると言えることになります。そして私たちが、このような画像認識タスクについてなら、そのような良いモデルになりうる関数を作る方法が存在することを基本的には理解していることは、重要な科学的事実なのです（それがどんな関数なのかはともかく）。
原注
では、そのような関数が正しく機能することを「数学的に証明」できるでしょうか？実は、無理なのです！
数学的に証明するためには、そもそも「人間の振る舞い」を数学的に説明しつくせる理論というものがなければ、手のつけようがありません。
先ほどの"2"の画像の例で、その画像にあるたくさんのピクセルのうち、ほんのいくつかのピクセル（の濃さ）だけを変更したらどうなるかを考えてみましょう。
「わずか数ピクセルの値だけが違う程度なら、その画像を"2"の画像だとみなしてやったって構わないじゃないか」とお思いになるかもしれませんが、肝心の「どこまでが"2"の画像であり、どこからが"2"の画像ではないか」という境目を決めているのは、結局「人間」の視覚がどのように感じるかなのです。人間にとって"2"に見えればそれは"2"であり、"2"に見えなければ"2"ではない、そういうことです。
これが人間の視覚ではなく、ハチ🐝やタコ🐙の視覚なら、明らかに違う答えになるでしょうし、エイリアン的な存在の視覚でも答えは異なるでしょう。
次回: （5/16）古典の「ニューラルネット」をおさらいする
概要
原文サイトのCreative Commons BY-NC-SA 4.0を継承する形で翻訳・公開いたします。
日本語タイトルは内容に即したものにしました。原文が長大なので、章ごとに16分割して公開します。
スタイルについては、かっこ書きを注釈にする、図をblockquoteにするなどフォーマットを適宜改善し、文面に適宜強調も加えています。
元記事は、2023年2月の公開時点における、ChatGPTを題材とした生成AIの基本概念について解説したものです。実際の商用AIでは有害コンテンツのフィルタなどさまざまな制御も加えられているため、そうした商用の生成AIが確率をベースとしつつ、確率以外の制御も加わっていることを知っておいてください。
本記事の原文を開いて、そこに掲載されている図版をクリックすると、自分のコンピュータでもすぐに実行して試せるWolfram言語コードが自動的にクリップボードにコピーされるようになっています。
コモンズ証 - 表示 - 非営利 - 継承 4.0 国際 - Creative Commons